Определение. Смешанным произведением трех векторов 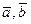 и
и 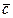 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 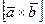 на вектор
на вектор 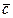 , т.е.
, т.е. 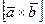 ·
· 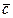 .
.
Свойства смешанного произведения:
1) смешанное произведение трех векторов равно нулю, если:
а) хотя бы один из перемноженных векторов равен нулю;
б) два из перемноженных векторов коллинеарны;
в) все три вектора параллельны одной и той же плоскости (компланарны).
2) смешанное произведение не изменится, если в нем поменять местами знаки векторного (×) и скалярного (·) умножения, т.е.
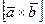 ·
· 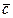 =
= 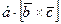 .
.
Объем V треугольной пирамиды, построенной на векторах 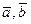 и
и 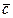 , вычисляется по формуле
, вычисляется по формуле
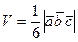 .
.
 2015-01-21
2015-01-21 480
480








