Определение 1. Функция 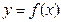 называется непрерывной в точке
называется непрерывной в точке 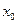 , если она определена в этой точке и некоторой ее окрестности, существует
, если она определена в этой точке и некоторой ее окрестности, существует 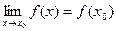 и этот предел равен значению функции в этой точке
и этот предел равен значению функции в этой точке 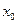 , т.е.
, т.е.
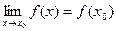 .
.
Пример. Проверим непрерывность функции 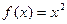 в произвольной точке
в произвольной точке 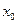 :
:
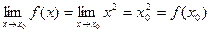 .
.
Приращением переменной величины будем называть разность между двумя ее различными значениями. Пусть в начальный момент времени переменная величина имела значение 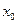 , а затем в процессе своего изменения приняла какое-то значение
, а затем в процессе своего изменения приняла какое-то значение 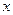 , разность
, разность 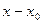 называется приращением этой переменной величины и обозначается
называется приращением этой переменной величины и обозначается 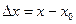 .
.
Приращение функции 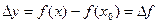 соответствует взятому приращению аргумента.
соответствует взятому приращению аргумента.
Определение 2. Функция 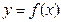 называется непрерывной в точке
называется непрерывной в точке 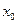 , если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента
, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента 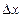 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 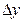 .
.
Теорема 1. Если функции 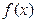 и
и 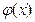 непрерывны в точке
непрерывны в точке 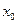 , то их сумма
, то их сумма 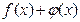 , разность
, разность 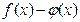 , произведение
, произведение 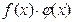 и частное
и частное 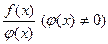 также непрерывны в этой точке.
также непрерывны в этой точке.
Теорема 2. Если промежуточный аргумент 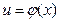 непрерывен в точке
непрерывен в точке 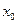 , а заданная функция
, а заданная функция 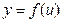 непрерывна в точке
непрерывна в точке 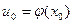 , то сложная функция
, то сложная функция 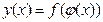 непрерывна в точке
непрерывна в точке 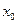 .
.
Теорема 3. Всякая элементарная функция непрерывна в любой точке своей области определения.
Если в точке 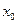 нарушены условия непрерывности функции
нарушены условия непрерывности функции 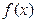 , то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
, то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
Определение. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной этой функции
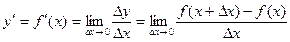 .
.
 2015-01-21
2015-01-21 701
701








