Иногда правила предельного перехода непосредственно неприменимы. Например, при отыскании 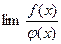 , когда
, когда 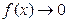 и
и 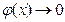 или одновременно
или одновременно 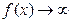 и
и 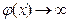 . В этом случае надо проделать над дробью некоторые преобразования. Чтобы обозначить такие ситуации, говорят, что имеем дело с неопределенностью
. В этом случае надо проделать над дробью некоторые преобразования. Чтобы обозначить такие ситуации, говорят, что имеем дело с неопределенностью 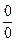 или
или 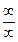 , а вычисление предела называют «раскрытием неопределенности».
, а вычисление предела называют «раскрытием неопределенности».
Пример 1. 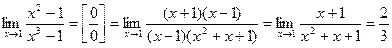 .
.
Пример 2. 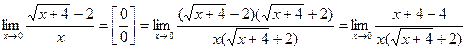 =
=
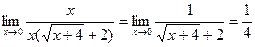 . (Чтобы убрать корни, умножили числитель и знаменатель на величину
. (Чтобы убрать корни, умножили числитель и знаменатель на величину 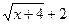 , сопряженную числителю).
, сопряженную числителю).
Пример 3. 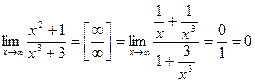 . (Поделили числитель и знаменатель дроби на старшую степень
. (Поделили числитель и знаменатель дроби на старшую степень 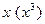 ).
).
«Неопределенности» могут возникнуть и при вычислении предела произведения 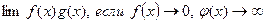 . Условно это записывается
. Условно это записывается 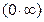 . Такую неопределенность легко преобразовать к
. Такую неопределенность легко преобразовать к 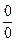 или
или 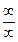 . Могут возникнуть также неопределенности вида
. Могут возникнуть также неопределенности вида 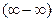 .
.
Пример 4. 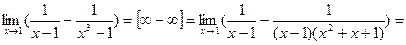
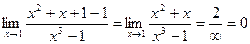 .
.
 2015-01-21
2015-01-21 441
441








