Пусть 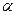 и
и 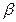 бесконечно малые (последовательности или функции).
бесконечно малые (последовательности или функции).
1) Если конечный и отличный от нуля предел существует
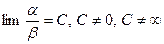 ,
,
то говорят, что 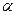 и
и 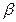 являются бесконечно малыми (б.м.) одного и того же порядка.
являются бесконечно малыми (б.м.) одного и того же порядка.
2) Если 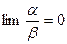 , то
, то 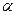 имеет высший порядок малости по отношению к
имеет высший порядок малости по отношению к 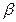 (или
(или 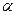 - б.м. более высокого порядка, чем
- б.м. более высокого порядка, чем 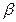 ).
).
3) Если 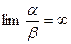 , то
, то 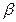 имеет высший порядок малости по отношению к
имеет высший порядок малости по отношению к 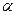 (или -
(или - 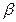 б.м. более высокого порядка, чем
б.м. более высокого порядка, чем 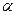 ).
).
4) Если 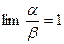 , то две бесконечно малые
, то две бесконечно малые 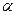 и
и 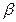 называются эквивалентными.
называются эквивалентными.
Таблица эквивалентных бесконечно малых при 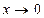
1. 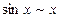 6.
6. 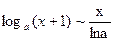
2. 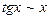 7.
7. 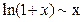
3. 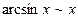 8.
8. 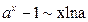
4. 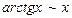 9.
9. 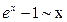
5. 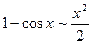 10.
10. 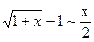
Пример. 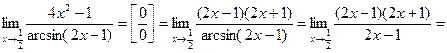
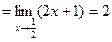 .
.
 2015-01-21
2015-01-21 463
463








