Таблица 3.1 – Основные характеристики ряда динамики
| Показатель | Цепной | Базисный |
| Абсолютный прирост | 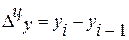 ,
где ,
где 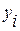 - уровень сравниваемого периода; - уровень сравниваемого периода;
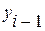 - уровень предшествующего периода. - уровень предшествующего периода.
| 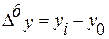 ,
где ,
где 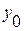 - уровень базисного периода. - уровень базисного периода.
|
Взаимосвязь: 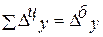
| ||
| Темп роста | 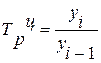
| 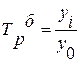
|
Взаимосвязь: 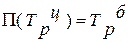
| ||
| Темп пророста | 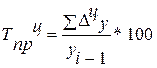
| 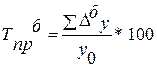 *100 *100
|
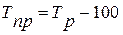 (в процентах) или (в процентах) или
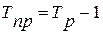 (в коэффициентах) (в коэффициентах)
| ||
| Абсолютное значение одного процента | 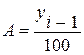
|
Таблица 3.2 – Средние показатели ряда динамики
| Показатель | Цепной | Базисный |
| Средний абсолютный прирост | 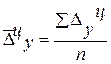 ,
где n – число цепных абсолютных приростов в изучаемом периоде. ,
где n – число цепных абсолютных приростов в изучаемом периоде.
| 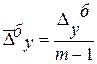 ,
где m – число уровней ряда динамики в изучаемом периоде, включая базисный. ,
где m – число уровней ряда динамики в изучаемом периоде, включая базисный.
|
| Средний темп роста | 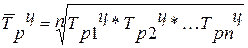 ,
где n – число цепных коэффициентов роста; ,
где n – число цепных коэффициентов роста;
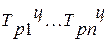 - цепные коэффициенты роста. - цепные коэффициенты роста.
|
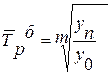
|
| Темп прироста | 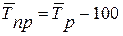 (в процентах) или (в процентах) или
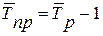 (в коэффициентах) (в коэффициентах)
|
Таблица 3.3 – Средний уровень ряда
| Ряд динамики | Формула среднего уровня ряда |
| Для интервальных рядов динамики из абсолютных уровней | |
| - при равных интервалах | 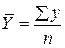 ,
где y – абсолютные уровни ряда;
n – число уровней ряда. ,
где y – абсолютные уровни ряда;
n – число уровней ряда.
|
| - при неравных интервалах | 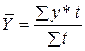 ,
где t – веса, длительность интервалов времени между смежными датами. ,
где t – веса, длительность интервалов времени между смежными датами.
|
| Для моментных рядов динамики | |
| - с равностоящими уровнями | 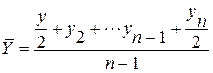
|
| - с неравностоящими уровнями | 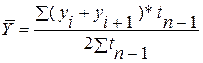
|
Таблица 3.4 – Измерение связи. Уравнения регрессии
| Линейная | 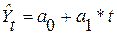 ,
где ,
где 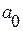 , , 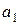 – параметры уравнения;
t- время. – параметры уравнения;
t- время.
|
| Гиперболическая | 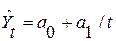
|
| Параболическая | 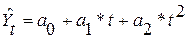
|
| Экспоненциальная | 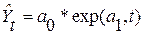
|
| Степенная | 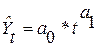
|
| Логарифмическая | 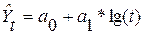
|
| Показательная | 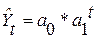
|
Параметры а0 и а1 определяются из системы уравнений:
а) линейная регрессия:
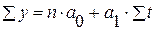
| |
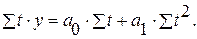
| (3.1) |
б) парабола второго порядка:
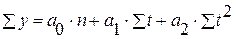
| |
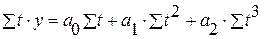
| |
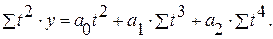
| (3.2) |
в) гипербола:
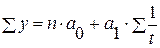
| |
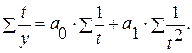
| (3.3) |
Для определения границ интервалов прогнозируемых явлений:
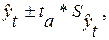
| (3.4) |
где 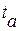 – коэффициент доверия по распределению Стьюдента;
– коэффициент доверия по распределению Стьюдента;
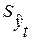 – остаточное среднее квадратическое отклонение от тренда:
– остаточное среднее квадратическое отклонение от тренда:
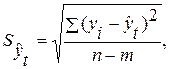
| (3.5) |
где m – число параметров адекватной модели тренда;
n – число уровней ряда динамики.
 2015-01-21
2015-01-21 613
613








