Задача № 3.2

Имеются данные об урожайности зерновых культур (исходные данные в столбцах 1 и 2):

Месяц	Фактическая урожайность, ц. (y)	Расчетные значения
t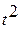
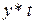
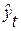
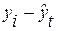
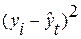
Январь	15,4	-9		-138,6	15,15	0,25	0,0625
Февраль	14,0	-7		-98,0	15,19	-1,19	1,4161
Март	17,6	-5		-88,0	15,23	2,37	5,6169
Апрель	15,4	-3		-46,2	15,28	0,12	0,0144
Май	10,9	-1		-10,9	15,32	-4,42	19,5364
Июнь	17,5			17,5	15,36	2,14	4,5796
Июль	15,0			45,0	15,4	-0,40	0,016
Август	18,5			92,5	15,45	3,05	9,3025
Сентябрь	14,2			99,4	15,49	-1,29	1,6641
Октябрь	14,9			134,1	15,53	-0,63	0,3969
Итого	153,4			6,8	153,4		42,6054

Определить урожайность на ноябрь текущего года, построив линейную трендовую модель.

Решение:

Для выравнивания ряда используем линейную трендовую модель –

уравнение прямой: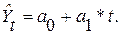

Параметры искомого уравнения прямой определяем из следующей системы нормальных уравнений:

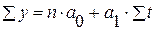
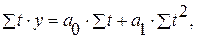откуда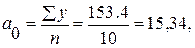

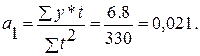
Уравнение прямой будет иметь вид: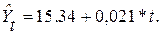

Подставляя в данной уравнение последовательно значения t, равные -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, находим выровненные уровни .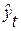

Если 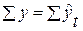, в нашем примере эти суммы равны между собой и равны 153,4, следовательно, значения уровней выровненного ряда найдены верно.

Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности зерновых культур в среднем на 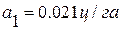в месяц.

Используя полученное уравнение методом экстраполяции при t равном 11, определяем ожидаемую урожайность культур на ноябрь текущего года:

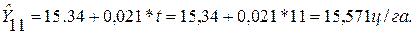
Зная точечную оценку прогнозируемого значения урожайности 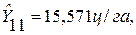, определяем вероятностные границы интервала по формуле:

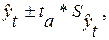
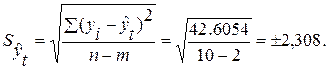
При доверительной вероятности, равной 0,95, коэффициент доверия Стьюдента равен 2,306.

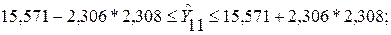
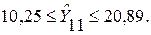
Таким образом, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в ноябре текущего года будет не менее чем 10,25, но и не более чем 20,89 ц/га.