На электроламповом заводе в порядке 5% механической выборки проверено 2000 лампочек, из которых 20 забраковано. Определить с вероятностью 0,997, в каких пределах колеблется процент бракованных лампочек.
Задача № 2.5
В порядке механической 5%-ой выборки было подвергнуто испытанию на разрыв 1000 нитей из партии. Установлено, что средняя крепость пряжи равняется 340 г при среднем квадратическом отклонении 20 г. С вероятностью 0,954 определите пределы, в которых находится средняя крепость пряжи в партии.
Задача № 2.6
В городе Н с числом семей 15000 предполагается методом случайного бесповторного отбора определить долю семей с детьми ясельного возраста. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,3.
Контрольные вопросы
1. Преимущества выборочного наблюдения перед сплошным.
2. Дать определение понятий: ошибка наблюдения, ошибка регистрации, ошибка репрезентативности, максимально возможная ошибка.
3. Условия правильного отбора единиц совокупности при выборочном наблюдении.
4. Генеральная и выборочная совокупности.
5. Различия между повторной и бесповторной выборками.
6. Формулы взаимосвязи средней и предельной ошибки выборки.
7. Формулы расчета средней ошибки при повторном и бесповторном отборе.
8. Неравенства, устанавливающие возможные пределы, в которых будут находиться характеристики генеральной совокупности.
9. Формулы для расчета необходимого объема выборки.
10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова.
11. Распространение результатов выборочного наблюдения на генеральную совокупность.
Тесты
1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется:
а) выборочной;
б) генеральной;
в) однородной;
г) свой ответ.
2. Виды ошибок статистических наблюдений:
а) регистрации;
б) систематические;
в) случайные;
г) репрезентативности;
д) все ответы верны.
3. По методу отбора различают:
а) бесповторный отбор;
б) случайный отбор;
в) повторный отбор;
г) все ответы верны.
4. Если количество единиц в совокупности меньше 30, то выборка считается:
а) большой;
б) малой;
в) средней;
г) нет верного ответа.
5. Виды выборок:
а) случайная;
б) типическая;
в) механическая;
г) групповая.
6. При 6%-ой выборке из партии деталей в 600 ед. объем выборки n составляет:
а) 54 ед;
б) 36 ед;
в) 46 ед.
7. Для характеристики надежности выборочных показателей различают следующие виды ошибок выборки:
а) среднюю;
б) случайную;
в) предельную;
г) репрезентативности.
8. Размер средней ошибки выборки зависит от:
а) объема выборки;
б) однородности совокупности;
в) ассиметрии;
г) степени варьирования изучаемого признака.
9. Чем больше численность выборки при прочих равных условиях, тем ________ величина средней ошибки выборки:
а) больше;
б) меньше;
в) точнее
г) свой ответ.
10. Чем больше вариация признака, тем ______ средняя ошибка выборки:
а) больше;
б) меньше;
в) точнее;
г) свой ответ.
11. Средняя ошибка выборки показывает __________.
12. Средняя ошибка выборки имеет единицы измерения:
а) что и количественный признак;
б) не имеет единиц измерения;
в) представлена коэффициентом;
г) в процентах.
13. Для отбора единиц из неоднородной совокупности применяется:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
14. Отбор единиц из генеральной совокупности посредством жеребьевки или какого-либо иного подобного способа – это:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
15. Доверительные интервалы (пределы) для средней ___________.
16. Для скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 22 дня со стандартным отклонением 6 дней.
Определить с вероятностью p равной 0,954 предельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.
а) 1,2 дня; 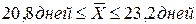 ;
;
б) 2,2 дня; 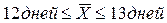 ;
;
в) 3 дня; 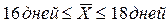 .
.
17. Среди выборочного обследования 1000 семей региона по уровню душевого дохода (выборка 2%-ая, механическая) малообеспеченных оказалось 300 семей.
Определить с вероятностью 0,997 долю малообеспеченных семей во всем регионе и доверительные интервалы.
а) 2%; 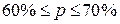 ;
;
б) 1,4%; 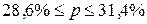 ;
;
в) 5%; 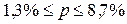 .
.
18. Для определения доли рабочих со стажем работы 20 лет и более на заводе с числом рабочих 10000 была проведена механическая выборка. Определить какова должна быть численность, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,05, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
а) 300 чел.;
б) 500 чел.;
в) 250 чел..
 2015-01-21
2015-01-21 1239
1239








