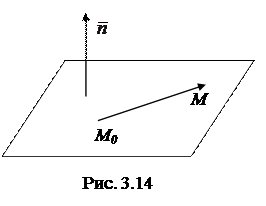
 Поставим следующую задачу. Требуется составить уравнение плоскости, проходящей через заданную точку
Поставим следующую задачу. Требуется составить уравнение плоскости, проходящей через заданную точку 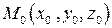 перпендикулярно заданному вектору
перпендикулярно заданному вектору 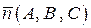 (см. рис.3.14). В дальнейшем вектор, перпендикулярный к плоскости мы будем называть нормальным вектором плоскости. Найдем геометрическое место точек
(см. рис.3.14). В дальнейшем вектор, перпендикулярный к плоскости мы будем называть нормальным вектором плоскости. Найдем геометрическое место точек 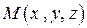 , принадлежащих плоскости. Для того, чтобы точка М принадлежала плоскости необходимо и достаточно, чтобы вектор
, принадлежащих плоскости. Для того, чтобы точка М принадлежала плоскости необходимо и достаточно, чтобы вектор 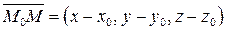 был перпендикулярен вектору
был перпендикулярен вектору 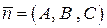 . Воспользуемся условием перпендикулярности векторов.
. Воспользуемся условием перпендикулярности векторов.
Напомним, что векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, т.е. 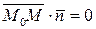 . В координатной форме имеем
. В координатной форме имеем
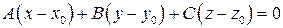 . (3.46)
. (3.46)
Раскрывая скобки в уравнении (3.46) и вводя обозначение 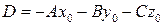 , мы получим общее уравнение плоскости:
, мы получим общее уравнение плоскости:
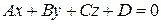 . (3.47)
. (3.47)
Если известны координаты трех точек 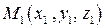 ,
, 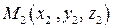 ,
, 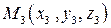 , не лежащих на одной прямой, то, используя условие компланарности трех векторов, можно составить уравнение плоскости, проходящей через эти заданные точки:
, не лежащих на одной прямой, то, используя условие компланарности трех векторов, можно составить уравнение плоскости, проходящей через эти заданные точки:
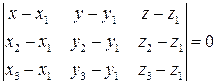 (3.48)
(3.48)
Напомним, что в общем уравнении плоскости коэффициенты при переменных являются координатами нормального вектора: 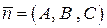 . Если заданы две плоскости
. Если заданы две плоскости 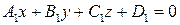 и
и 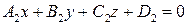 , то угол между ними равен углу между их нормальными векторами
, то угол между ними равен углу между их нормальными векторами 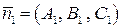 и
и 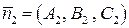 .
.
Для нахождения угла между плоскостями воспользуемся формулой (2.5)
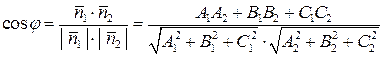 . (3.49)
. (3.49)
Пример 3.7. Требуется найти угол между плоскостями 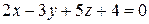 и
и 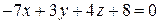 .
.
Нормальными векторами данных плоскостей являются следующие векторы 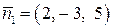 и
и 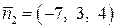 . Подставим координаты этих векторов в формулу (3.49):
. Подставим координаты этих векторов в формулу (3.49):
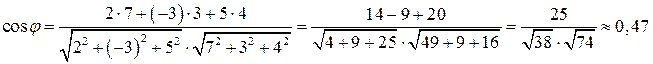 .
.
Следовательно, 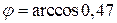 .
.
Заметим, что в общем уравнении прямой на плоскости 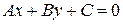 коэффициенты при переменных так же являются координатами вектора, перпендикулярного данной прямой (нормального вектора) и лежащего в той же плоскости xOy. Угол между двумя прямыми на плоскости
коэффициенты при переменных так же являются координатами вектора, перпендикулярного данной прямой (нормального вектора) и лежащего в той же плоскости xOy. Угол между двумя прямыми на плоскости 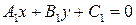 и
и 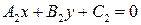 можно найти по формуле, полученной из формулы (2.5), если в ней третьи координаты векторов положить равными нулю:
можно найти по формуле, полученной из формулы (2.5), если в ней третьи координаты векторов положить равными нулю:
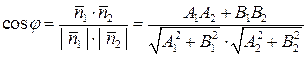 . (3.50)
. (3.50)
Прямая линия в пространстве может быть задана как пересечение двух плоскостей:
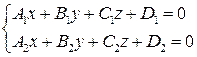 . (3.51)
. (3.51)
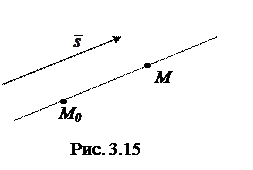 Уравнения (3.51) называются общими уравнениями прямой в пространстве. Поставим теперь другую задачу. Пусть требуется составить уравнения прямой в пространстве, проходящей через заданную точку
Уравнения (3.51) называются общими уравнениями прямой в пространстве. Поставим теперь другую задачу. Пусть требуется составить уравнения прямой в пространстве, проходящей через заданную точку 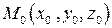 параллельно заданному вектору
параллельно заданному вектору 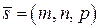 (см. рис. 3.15). Вектор
(см. рис. 3.15). Вектор 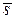 называется направляющим вектором прямой. Найдем геометрическое место точек
называется направляющим вектором прямой. Найдем геометрическое место точек 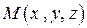 , принадлежащих прямой. Для того, чтобы точка М принадлежала прямой необходимо и достаточно, чтобы векторы
, принадлежащих прямой. Для того, чтобы точка М принадлежала прямой необходимо и достаточно, чтобы векторы 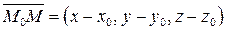 и
и 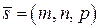 лежали на параллельных прямых (такие векторы называются коллинеарными). Напомним, что у коллинеарных векторов координаты пропорциональны, т.е.
лежали на параллельных прямых (такие векторы называются коллинеарными). Напомним, что у коллинеарных векторов координаты пропорциональны, т.е.
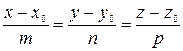 . (3.52)
. (3.52)
Система уравнений (3.52) называется каноническими уравнениями прямой линии в пространстве. Канонические уравнения прямой можно использовать только в том случае, когда все координаты направляющего вектора 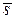 отличны от нуля. Если известны две точки
отличны от нуля. Если известны две точки 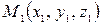 и
и 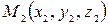 , через которые проходит прямая, то в качестве направляющего вектора данной прямой можно взять вектор
, через которые проходит прямая, то в качестве направляющего вектора данной прямой можно взять вектор 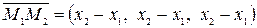 . В этом случае уравнения (3.52) превращается в уравнения прямой, проходящей через две заданные точки:
. В этом случае уравнения (3.52) превращается в уравнения прямой, проходящей через две заданные точки:
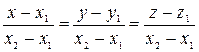 (3.53)
(3.53)
Угол между двумя прямыми, заданными каноническими уравнениями
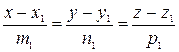 ,
,
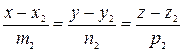
равен углу между их направляющими векторами 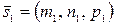 и
и 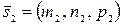 .
.
Для нахождения угла между двумя прямыми воспользуемся формулой (2.5)
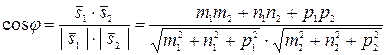 (3.54)
(3.54)
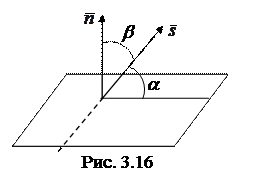
Угол a между прямой 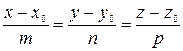 и плоскостью
и плоскостью 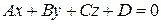 можно найти как угол, дополнительный к углу b, образованному нормальным вектором плоскости
можно найти как угол, дополнительный к углу b, образованному нормальным вектором плоскости 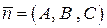 и направляющим вектором прямой
и направляющим вектором прямой 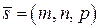 (рис. 3.16).
(рис. 3.16).
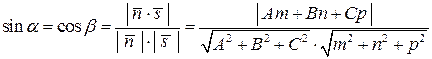 . (3.55)
. (3.55)
Модуль в числителе объясняется тем, что угол a между прямой и плоскостью всегда является острым (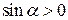 ).
).
Задача 3.8. Определить угол между плоскостью 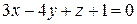 и прямой, проходящей через точки
и прямой, проходящей через точки 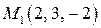 и
и 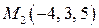 .
.
Решение. Координаты нормального вектора плоскости совпадают с коэффициентами ее уравнения: 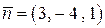 . Направляющий вектор прямой
. Направляющий вектор прямой 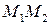 равен
равен 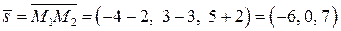 .
.
Искомый угол a находимпо формуле (3.55):
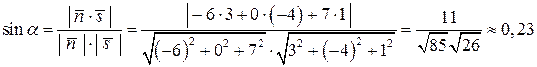 .
.
Следовательно, 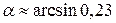 .
.
Ч А С Т Ь II
 2015-04-01
2015-04-01 1788
1788
