2015-01-21
1069
Для того, чтобы ввести фиктивную переменную в регрессионную модель, ей необходимо присвоить некоторые числовые значения, придав тем самым фиктивным переменным количественное содержание. В случае дихотомической переменной это делается следующим образом. Фиктивной переменной придается значение 1, если признак присутствует в наблюдении, и 0 – при его отсутствии. Таким образом, если z – дихотомическая переменная, то в описанном выше двоичном виде она формализуется равенством
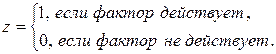
Что касается фиктивной переменой, имеющей k уровней качества (k > 2), то при построении регрессионной модели она заменяется на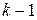 
дихотомическую фиктивную переменную.
Например, при исследовании зависимости заработной платы от стажа работника и его образования модель может быть представлена в виде:
,
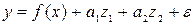где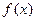 
– часть заработной платы, объясняемая стажем,
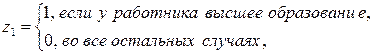
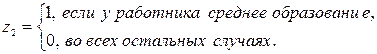
Третьей дихотомической переменной z 3 и не требуется, так как если работник имеет начальное образование, то это уже учтено при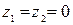 
. Более того, с точки зрения требований к качеству модели ее вводить нельзя, так как тогда для любого работника
|
|
|
z 1 + z 2 + z 3= 1,
то есть переменные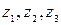 
становятся линейно зависимыми, а это приводит к появлению мультиколлинеарности. Такая ситуация совершенной мультиколлинеарности получила название «ловушка фиктивной переменной». Чтобы избежать ее, необходимо руководствоваться следующим простым правилом.
Если фиктивная переменная z имеет k качественных уровней, то при моделировании вместо нее используются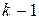 
дихотомическая переменная z 1, z 2, …, zk- 1.
