Анализ структурной стабильности тенденции

От сезонных и циклических колебаний, оказывающих систематическое влияние на характер тенденции, отличаются структурные сдвиги – аномальные движения временного ряда, которые связаны с редко происходящими экономическими событиями, имеют скачкообразный характер и меняют тенденцию. К событиям, вызывающим структурные сдвиги, можно отнести, например, начало нового экономического курса, топливно-энергетические и финансовые кризисы, смену экономической ситуации в исследуемой области, а также другие факторы глобального характера.

В результате структурного сдвига, начиная с некоторого момента времени t, происходит изменение в развитии самого изучаемого показателя, а следовательно, изменяется поведение тренда, описывающего его развитие, например, на смену линейному характеру развития приходит кусочно-линейный.

Для моделирования ситуаций с изменением поведения тенденции, существуют специальные математические приемы. Один из них связан с применением теста Чоу, описанного в главе 4.

Суть теста Чоу для анализа структурной стабильности тенденции заключается в следующем:

1) полный временной ряд 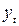длины n разбивается на две приблизительно равные части длины 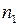и ();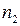

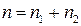2) для полного временного ряда и его частей оцениваются параметры линейных уравнений тренда: , , ;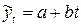

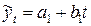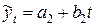3) выдвигается и проверяется с помощью F -статистики гипотеза о структурной стабильности тенденции, а именно гипотеза .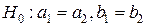

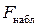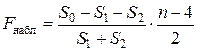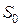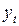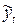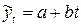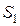Наблюдаемое значение статистики вычисляется по выборочным данным на основании формулы , где – сумма квадратов отклонений уровней полного временного ряда от соответствующих значений , рассчитанных по уравнению регрессии , а и 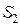– суммы квадратов отклонений уровней частей временного ряда 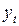от соответствующих теоретических значений, рассчитанных по уравнениям 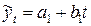и .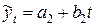

Рассматриваемая F -статистика имеет распределение Фишера с числами степеней свободы 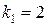и 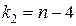. Если 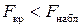, то гипотеза 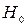отклоняется. В этом случае моделирование тренда следует осуществлять с помощью кусочно-линейной модели. Если же 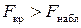, то нет оснований отклонять нулевую гипотезу, а значит, моделирование тренда следует осуществлять с помощью единого для всего временного ряда уравнения .

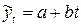Графическая интерпретация выводов тестирования заключается в следующем. Если 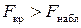, то по заданному корреляционному полю единая прямая хорошо моделирует ситуацию (рис. 6.9). Если же 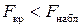, то по тому же корреляционному полю (рис. 6.10) следует отдать предпочтение моделированию с помощью некоторой ломаной линии.

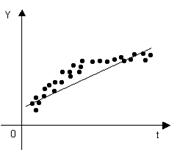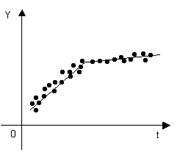Рис. 6.9. Модель, представленная единой прямой	Рис. 6.10. Модель, представленная ломаной линией