Пример 6.1. В таблице 6.3 приведены данные об уровнях временного ряда. Проверить с помощью метода Ирвина наличие аномальных уровней.
Таблица 6.3. Данные примера 6.1
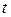 | ||||||||||
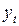 | 1,6 | 1,9 | 2,1 | 2,4 | 4,5 | 2,8 | 3,1 | 3,3 | 3,6 | 3,8 |
Решение:
На рисунке 6.11 приведен точечный график временного ряда.
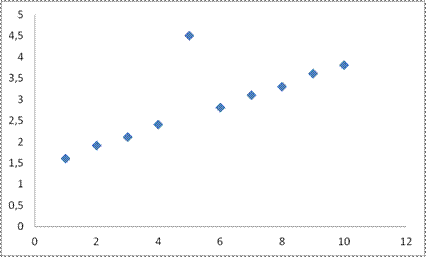
Рис. 6.11. График временного ряда
Из графика временного ряда можно сделать вывод, что пятому наблюдению временного ряда соответствует резкий выброс. Исследуем точку 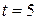 на аномальное значение.
на аномальное значение.
Для нахождения наблюдаемого значения критерия Ирвина воспользуемся формулой 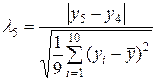 .
.
Так как 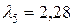 и
и 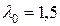 , то
, то 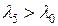 , а значит, уровень
, а значит, уровень 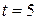 является аномальным. Если аномалия уровня вызвана ошибками первого рода, то пятый уровень можно заменить на среднее арифметическое четвертого и шестого уровней, т.е. на значение
является аномальным. Если аномалия уровня вызвана ошибками первого рода, то пятый уровень можно заменить на среднее арифметическое четвертого и шестого уровней, т.е. на значение 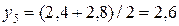 .
.
Пример 6.2. В таблице 6.4 приведены поквартальные данные об объемах производства некоторого предприятия. С помощью анализа автокорреляционной функции и графика временного ряда определить структуру временного ряда.
Таблица 6.4. Данные примера 6.2
| Год | Квартал | Период | Объем производства, млрд. руб.,  |
Решение:
Вычислим коэффициенты автокорреляции первого, второго, третьего, четвертого и пятого порядков.
Для вычисления коэффициента автокорреляции первого порядка по данным таблицы 6.5 найдем корреляцию между рядами  , где
, где 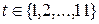 , и
, и 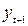 , где
, где 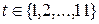 .
.
Тогда 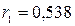 .
.
Таблица 6.5. Данные для расчета коэффициента автокорреляции
первого порядка
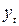 | 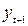 |
Для вычисления коэффициента автокорреляции второго порядка по данным таблицы 6.6 найдем корреляцию между рядами 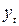 , где
, где 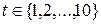 , и
, и 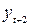 , где
, где 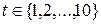 .
.
Таблица 6.6. Данные для расчета коэффициента автокорреляции
второго порядка
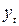 | 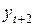 |
Тогда 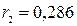 .
.
Аналогично рассчитываются коэффициенты автокорреляции третьего, четвертого и пятого порядков: 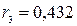 ,
, 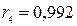 ,
, 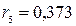 .
.
Так как из последовательности коэффициентов автокорреляции 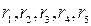 самым высоким оказался коэффициент
самым высоким оказался коэффициент 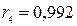 , то можно сделать вывод о том, что исследуемый временной ряд содержит периодические (сезонные) колебания с периодом, равным 4. Кроме того, из вида графика временного ряда (рисунок 6.12) можно сделать вывод о наличии тренда.
, то можно сделать вывод о том, что исследуемый временной ряд содержит периодические (сезонные) колебания с периодом, равным 4. Кроме того, из вида графика временного ряда (рисунок 6.12) можно сделать вывод о наличии тренда.
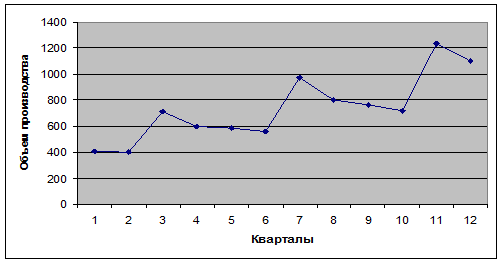
Рис. 6.12. График временного ряда
Пример 6.3. С помощью метода сравнения средних уровней определить наличие тренда во временном ряду 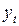 , заданном таблицей 6.7.
, заданном таблицей 6.7.
Таблица 6.7. Данные примера 6.3
| Период | ||||||||
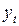 | 14,1 | 9,3 | 19,4 | 19,7 | 5,4 | 24,2 | 13,8 | 24,5 |
| Период | - | |||||||
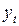 | 14,7 | 16,6 | 5,6 | 16,2 | 25,3 | 11,9 | 18,5 | - |
Решение:
Из вида корреляционного поля (рисунок 6.13) трудно сделать однозначный вывод о наличии или отсутствии тренда в заданном временном ряду.
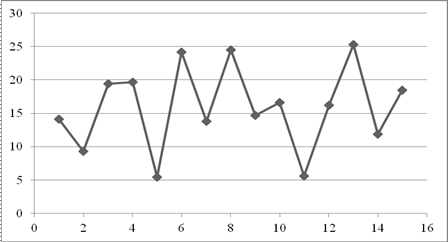
Рис. 6.13. График временного ряда
Для определения тренда применим метод сравнения средних уровней.
Разделим временной ряд на две части длины 7 и 8 соответственно. Оценим среднее и дисперсию первой и второй частей временного ряда: 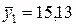 ,
, 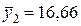 ,
, 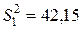 ,
, 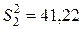 .
.
Проверяем гипотезу о равенстве (однородности) дисперсий обеих частей ряда с помощью F -критерия Фишера. Для вычисления наблюдаемого значения F -критерия большую дисперсию разделим на меньшую: 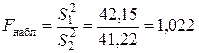 . Табличное значение
. Табличное значение 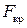 статистики Фишера при уровне значимости
статистики Фишера при уровне значимости 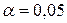 и числе степеней свободы
и числе степеней свободы 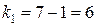 ,
, 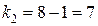 составляет 3,87.
составляет 3,87.
Так как 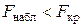 , то c вероятностью 95% нет оснований отвергать нулевую гипотезу. По данным наблюдений выборочные дисперсии различаются незначимо (расхождение между ними случайно). Значит, выделенные части временного ряда можно считать однородными.
, то c вероятностью 95% нет оснований отвергать нулевую гипотезу. По данным наблюдений выборочные дисперсии различаются незначимо (расхождение между ними случайно). Значит, выделенные части временного ряда можно считать однородными.
Проверим основную гипотезу о равенстве средних значений с использованием t-критерия Стьюдента:
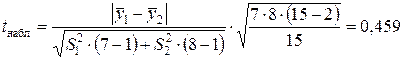 ,
, 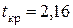 .
.
Так как 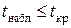 , то нет оснований отвергать нулевую гипотезу о равенстве средних, а значит, расхождение между вычисленными средними незначимо. Отсюда следует, что тренд во временном ряду
, то нет оснований отвергать нулевую гипотезу о равенстве средних, а значит, расхождение между вычисленными средними незначимо. Отсюда следует, что тренд во временном ряду 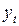 отсутствует.
отсутствует.
Пример 6.4. В таблице 6.8 отражены данные некоторой фирмы об объемах продаж товара.Подобрать линию тренда, которая лучше всего описывает фактические данные и на ее основе сделать прогноз на 3 недели вперед.
Таблица 6.8. Данные примера 6.4
| Неделя | |||||||||||
| Количество проданных единиц |
Решение:
1. Ввод исходных данных задачи. В ячейки A1 и B1 введем заголовки исходных данных, в ячейки A2:A12 – номера недель, а в ячейки B2:B12 – соответствующее количество продаж.
2. Построение графика фактических значений показателя. Выделим ячейки B1:B12 (исходные данные вместе с заголовком) и нажмем кнопку Мастер диаграмм на панели инструментов. Построим с его помощью диаграмму типа График (рисунок 6.14).
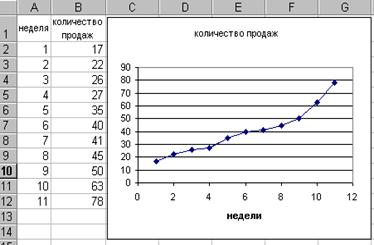
Рис. 6.14. График продаж
3. Изображение на графике кривой роста линейной модели. Выполним один щелчок по диаграмме для того, чтобы перейти в режим ее редактирования. Затем подведем курсор к какой-либо точке на графике и снова щелкнем левой кнопкой мыши. Нажмем правую кнопку мыши для вызова контекстного меню. В контекстном меню выберем команду Добавить линию тренда (рисунок 6.15).
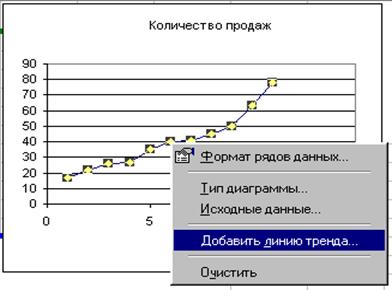
Рис. 6.15. Схема выбора меню Добавить линию тренда
На экране появляется окно Линия тренда (рисунок 6.16).
Рис. 6.16. Окно Линия тренда
В окне Линия тренда на вкладке Тип выберем Линейная, а на вкладке Параметры установим следующие флажки:
· показывать уравнение на диаграмме;
· поместить на диаграмму величину индекса детерминации (R ^2).
После нажатия кнопки OK на графике наряду с фактическими значениями количества продаж будет показана линия тренда, уравнение и коэффициент детерминации (рисунок 6.17).
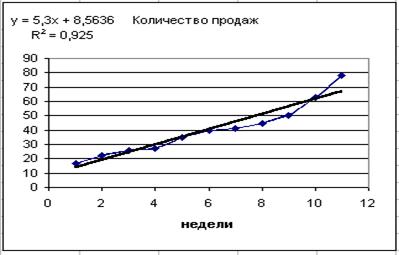
Рис. 6.17. График линейного тренда
4. Подбор функции тренда, наиболее точно описывающей исходные данные. Аналогично следует испытать другие типы линий тренда. При добавлении каждой новой линии тренда на график нужно сравнить ее коэффициент детерминации с аналогичным показателем предыдущей модели. В результате перебора всех возможных (стандартных) линий тренда в данной задаче выбор останавливается на экспоненциальной модели, поскольку для нее коэффициент детерминации наибольший (рисунок 6.18).
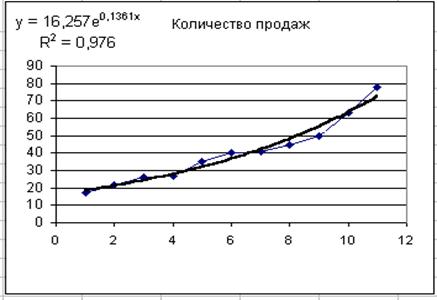
Рис. 6.18. График экспоненциального тренда
5. Выполнение прогноза. Поскольку нужно выполнить прогноз на 3 недели вперед, допишем номера этих недель (12, 13 и 14) в столбец A. В соответствующие ячейки в столбце B занесем формулы вычисления теоретического значения по функции тренда. Так как уравнение экспоненциальной кривой имеет вид 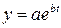 , то для расчетов необходимо использовать функцию EXP(), т.е. в ячейку B13 нужно записать формулу
, то для расчетов необходимо использовать функцию EXP(), т.е. в ячейку B13 нужно записать формулу
=16,257*EXP(0,1361*A13).
Затем эту формулу можно скопировать в ячейки B14 и B15. В результате получим в ячейках B13:B15 следующие прогнозные значения:
· на 12-ю неделю – 83 продажи;
· на 13-ю неделю – 95 продаж;
· на 14-ю неделю – 109 продаж.
Пример 6.5. Имеются статистические данные (таблица 6.9) об объемах выпуска продукции  (млрд. руб.) на некотором предприятии за несколько лет.
(млрд. руб.) на некотором предприятии за несколько лет.
Таблица 6.9. Данные примера 6.5
| Год | |||||||||
 |
Проверить, имеется ли тенденция в изменении выпуска продукции. Выбрать тип тренда и рассчитать его параметры. Проверить качество построенной модели. Сделать точечный и интервальный прогнозы на 2009 год.
Решение:
Построим график выпуска продукции (рисунок 6.19). По виду диаграммы можно предположить, что во временном ряду присутствует линейный тренд.
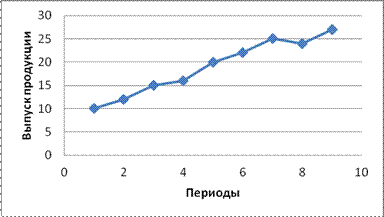
Рис. 6.19. График выпуска продукции
Конечно, выбор тренда можно осуществить и экспериментальным методом. При этом индекс детерминации у полиномиального тренда несколько выше, но выбор остановим на линейном тренде ввиду его простоты и ясной экономической интерпретации параметров регрессии.
Оценим параметры тренда методом наименьших квадратов. В качестве значений независимой переменной возьмем значения периодов.
Уравнение линейной регрессии имеет вид 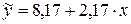 . Коэффициент при переменной
. Коэффициент при переменной 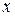 показывает, что за один год выпуск продукции на предприятии увеличивается в среднем на 2,17 млрд. руб.
показывает, что за один год выпуск продукции на предприятии увеличивается в среднем на 2,17 млрд. руб.
Общее качество уравнения регрессии высокое (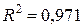 ).
).
Оценим статистическую значимость индекса детерминации. В нашем случае 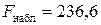 ,
, 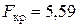 . Так как
. Так как 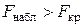 , то уравнение регрессии в целом статистически значимо.
, то уравнение регрессии в целом статистически значимо.
Для коэффициентов регрессии модули наблюдаемых значений статистики Стьюдента (10,3 и 15,4) больше критического значения, равного 2,36. Значит, коэффициенты регрессии статистически значимы.
Точность модели оценим с помощью коэффициента аппроксимации 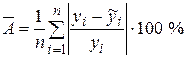 . В нашем случае он составляет 4,34%, что говорит о высокой точности модели.
. В нашем случае он составляет 4,34%, что говорит о высокой точности модели.
Так как среднее значение остатков (равное -9,86865E-16) является несмещенной оценкой математического ожидания, то можно считать (не прибегая к статистическим тестам), что математическое ожидание случайного члена равно нулю и первое условие теоремы Гаусса-Маркова.
Так как модель построена по данным временного ряда, она гомоскедастична.
Проверим модель на автокорреляцию. Для этого воспользуемся критерием Дарбина-Уотсона. Вычислим наблюдаемое значение статистики: 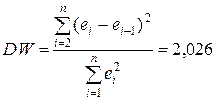 . Критические значения статистики имеют следующие значения: d 1 =0,824; d 2 =1,32. Так как наблюдаемое значение попадает в зону отсутствия автокорреляции, то соответствующее условие теоремы Гаусса-Маркова об отсутствии автокорреляции выполняется.
. Критические значения статистики имеют следующие значения: d 1 =0,824; d 2 =1,32. Так как наблюдаемое значение попадает в зону отсутствия автокорреляции, то соответствующее условие теоремы Гаусса-Маркова об отсутствии автокорреляции выполняется.
Исследование ряда остатков показывает адекватность и надежность построенной модели.
Выберем 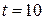 (соответствует 2009-ому году) и подставим в уравнение тренда. Получим точечный прогноз, равный 29,8 (млрд. руб.).
(соответствует 2009-ому году) и подставим в уравнение тренда. Получим точечный прогноз, равный 29,8 (млрд. руб.).
Для интервального прогнозапо модели предварительно рассчитаем стандартную ошибку прогноза:
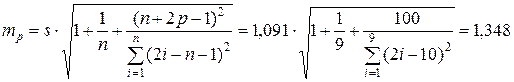 ,
,
где 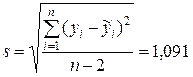 и
и 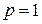 ,
, 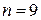 .
.
Затем по значениям 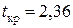 ,
, 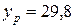 и
и 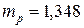 строится доверительный интервал прогноза
строится доверительный интервал прогноза 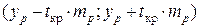 , т.е. определяются нижняя и верхняя границы интервала прогноза. В нашем случае эти границы имеют значения 26,62 и 32,98.
, т.е. определяются нижняя и верхняя границы интервала прогноза. В нашем случае эти границы имеют значения 26,62 и 32,98.
Пример 6.6. По статистическим данным РУП «Белоруснефть-Минскоблнефтепродукт» ( таблица 6.10) о реализации дизельного топлива
организациям и предприятиям Минска и Минской области в 2004-2010 годах:
1) построить график реализации дизельного топлива;
2) провести анализ структуры временного ряда;
3) смоделировать тренд временного ряда;
4) рассчитать значения сезонной компоненты;
5) построить график модели временного ряда;
6) оценить точность модели с помощью ошибки аппроксимации.
Таблица 6.10. Данные примера 6.6
| 2004 год | 2005 год | 2006 год | 2007 год | 2008 год | 2009 год | 2010 год | |
| январь | 5 656,5 | 5 322,6 | 7 555,6 | 11 283,5 | 15 369,9 | 15 232,7 | 16 122,2 |
| февраль | 4 575,1 | 5 963,0 | 7 700,9 | 8 630,4 | 13 775,8 | 15 256,1 | 18 212,8 |
| март | 10 524,8 | 10 501,8 | 10 368,0 | 8 677,2 | 20 710,9 | 16 086,6 | 21 044,2 |
| апрель | 24 638,2 | 19 879,1 | 13 724,0 | 21 442,1 | 29 942,0 | 31 164,5 | 34 991,5 |
| май | 8 948,6 | 12 874,2 | 13 110,3 | 15 089,4 | 24 888,2 | 23 869,4 | 28 488,6 |
| июнь | 11 098,6 | 14 624,8 | 15 369,7 | 18 561,8 | 27 098,9 | 21 392,0 | 29 021,1 |
| июль | 11 717,2 | 14 250,0 | 21 332,0 | 28 819,5 | 29 186,0 | 26 125,8 | 35 921,0 |
| август | 25 471,9 | 26 119,8 | 25 174,5 | 23 840,2 | 41 018,0 | 40 182,8 | 36 633,5 |
| сентябрь | 15 656,3 | 20 347,7 | 16 643,6 | 24 188,4 | 27 176,0 | 26 594,7 | 33 083,1 |
| октябрь | 11 659,1 | 15 497,3 | 14 487,9 | 21 821,1 | 28 725,7 | 26 129,8 | 31 881,8 |
| ноябрь | 9 440,5 | 10 225,2 | 14 739,6 | 16 209,7 | 19 275,5 | 18 995,2 | 27 850,2 |
| декабрь | 6 120,0 | 8 471,3 | 13 303,0 | 15 871,4 | 18 229,9 | 18 567,1 | 23 300,6 |
Решение:
1) По данным, представленным в таблице 6.10, построим график (рисунок 6.20).
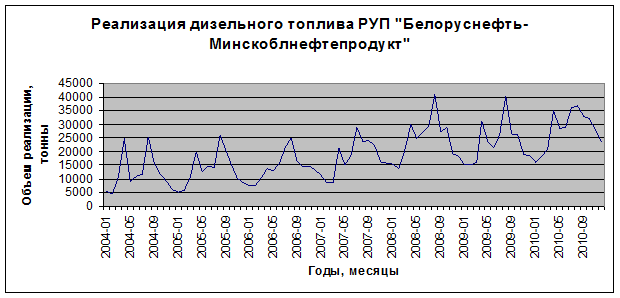
Рис. 6.20. График объемов реализации дизельного топлива
Визуальный анализ графика позволяет предположить, что в структуре временного ряда присутствует тренд и периодическая компонента.
2) Гипотеза о наличии во временном ряду тренда и цикличности подтверждается анализом автокорреляционной функции (таблица 6.11) и видом коррелограммы (рисунок 6.21).
Таблица 6.11. Значения коэффициентов автокорреляции
Величина лага 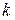 | Значение 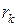 | Величина лага 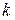 | Значение 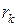 |
| 0,71702083 | 0,651380855 | ||
| 0,54776565 | 0,46330488 | ||
| 0,408553694 | 0,308968907 | ||
| 0,374505412 | 0,249877841 | ||
| 0,16680431 | 0,021476034 | ||
| 0,098540112 | -0,041952295 | ||
| 0,083549887 | -0,022349169 | ||
| 0,278848046 | 0,180584117 | ||
| 0,346140315 | 0,314749942 | ||
| 0,48576767 | 0,466136492 | ||
| 0,664128668 | 0,63515393 | ||
| 0,863952903 | 0,797762771 |
Так как самыми высокими являются двенадцатый и двадцать четвертый коэффициенты автокорреляции, то временной ряд содержит сезонную компоненту с периодом 12.
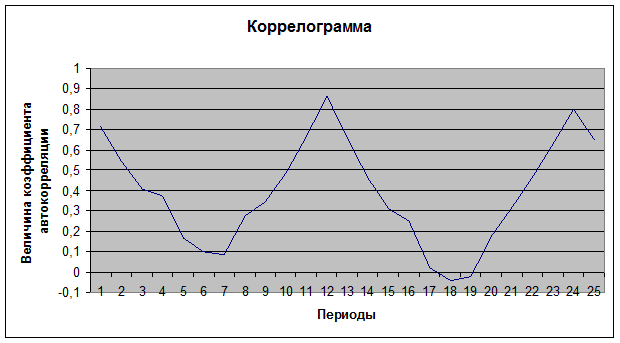
Рис. 6.21. Коррелограмма
3) Для моделирования тренда временного ряда воспользуемся экспериментальным методом. Для этого построим и сравним между собой несколько трендов, полученных на основе аналитического выравнивания (рисунки 6.22-6.26).
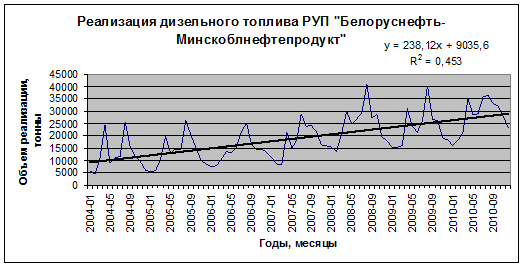
Рис. 6.22. График линейного тренда
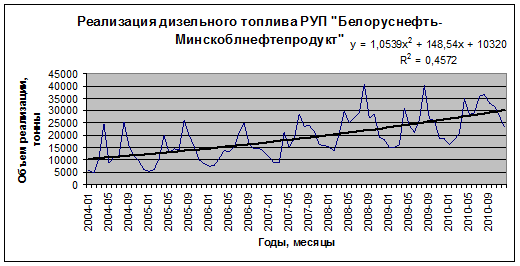
Рис. 6.23. График полиномиального тренда
Сравнивая индексы детерминации для линейной (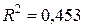 ), полиномиальной (
), полиномиальной (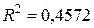 ), степенной (
), степенной (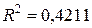 ), логарифмической (
), логарифмической (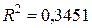 ) и экспоненциальной (
) и экспоненциальной (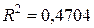 ) функций, выбираем линейный тренд
) функций, выбираем линейный тренд 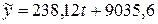 (ввиду его простоты и четкой экономической интерпретации коэффициентов регрессии). Из уравнения линейного тренда следует, что в среднем объем реализации дизельного топлива ежемесячно увеличивается на 238,12 тонны.
(ввиду его простоты и четкой экономической интерпретации коэффициентов регрессии). Из уравнения линейного тренда следует, что в среднем объем реализации дизельного топлива ежемесячно увеличивается на 238,12 тонны.
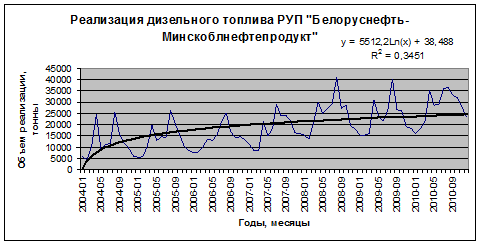
Рис. 6.24. График логарифмического тренда
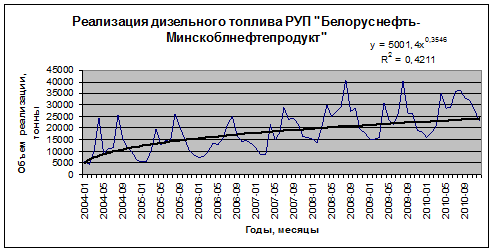
Рис. 6.25. График степенного тренда
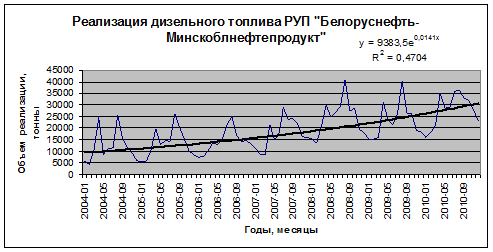
Рис. 6.26. График экспоненциального тренда
4) Из графика временного ряда следует также, что амплитуда колебаний со временем изменяется слабо. Поэтому в качестве итоговой формы модели временного ряда следует выбрать аддитивную форму.
Такой выбор при моделировании циклических колебаний предполагает использование абсолютных отклонений 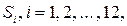 фактического ряда от выровненного по каждому из двенадцати месяцев (в качестве выровненного ряда выбирается последовательность соответствующих значений линейного тренда
фактического ряда от выровненного по каждому из двенадцати месяцев (в качестве выровненного ряда выбирается последовательность соответствующих значений линейного тренда 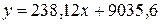 ). Расчет абсолютных отклонений
). Расчет абсолютных отклонений 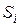 ,
, 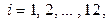 осуществляется по формуле
осуществляется по формуле
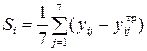 ,
,
где 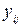 – значение исходного временного ряда для
– значение исходного временного ряда для 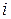 -ого месяца в
-ого месяца в 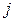 -ом году,
-ом году, 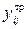 – значение линейного тренда
– значение линейного тренда 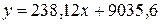 для
для 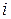 -ого месяца в
-ого месяца в 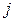 -ом году. Все результаты соответствующих вычислений сведены в таблице 6.12. Так как корректировочный коэффициент сезонности
-ом году. Все результаты соответствующих вычислений сведены в таблице 6.12. Так как корректировочный коэффициент сезонности 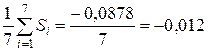 близок к нулю, то корректировка значений сезонной компоненты не производится.
близок к нулю, то корректировка значений сезонной компоненты не производится.
Таблица 6.12. Значения средних абсолютных отклонений
| Месяц | Среднее абсолютное отклонение от тренда 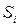 |
| январь | -6911,33 |
| февраль | -7496,43 |
| март | -4334,64 |
| апрель | 6551,229 |
| май | -617,277 |
| июнь | 558,6314 |
| июль | 4632,597 |
| август | 11692,93 |
| сентябрь | 3633,257 |
| октябрь | 1468,409 |
| ноябрь | -3550,68 |
| декабрь | -5627,75 |
5) Далее с учетом выбора аддитивной формы модели пересчитываются теоретические значения. Для этого складываются соответствующие значения тренда и средние абсолютные отклонения от него (таблица 6.13).
Таблица 6.13. Теоретические значения модельного временного ряда
| 2004 год | 2005 год | 2006 год | 2007 год | 2008 год | 2009 год | 2010 год |
| 2362,394 | 5219,834 | 8077,274 | 10934,71 | 13792,15 | 16649,59 | 19507,03 |
| 2015,409 | 4872,849 | 7730,289 | 10587,73 | 13445,17 | 16302,61 | 19160,05 |
| 5415,323 | 8272,763 | 11130,2 | 13987,64 | 16845,08 | 19702,52 | 22559,96 |
| 16539,31 | 19396,75 | 22254,19 | 25111,63 | 27969,07 | 30826,51 | 33683,95 |
| 9608,923 | 12466,36 | 15323,8 | 18181,24 | 21038,68 | 23896,12 | 26753,56 |
| 11022,95 | 13880,39 | 16737,83 | 19595,27 | 22452,71 | 25310,15 | 28167,59 |
| 15335,04 | 18192,48 | 21049,92 | 23907,36 | 26764,8 | 29622,24 | 32479,68 |
| 22633,49 | 25490,93 | 28348,37 | 31205,81 | 34063,25 | 36920,69 | 39778,13 |
| 14811,94 | 17669,38 | 20526,82 | 23384,26 | 26241,7 | 29099,14 | 31956,58 |
| 12885,21 | 15742,65 | 18600,09 | 21457,53 | 24314,97 | 27172,41 | 30029,85 |
| 8104,237 | 10961,68 | 13819,12 | 16676,56 | 22391,44 | 25248,88 | |
| 6265,294 | 9122,734 | 11980,17 | 14837,61 | 17695,05 | 20552,49 | 23409,93 |
Построенная по этим данным аддитивная модель временного ряда имеет графическое изображение, представленное на рисунке 6.27.
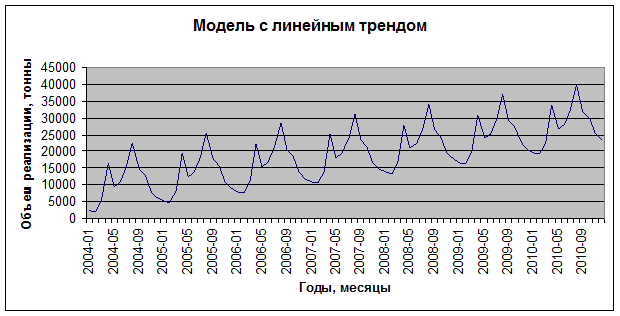
Рис. 6.27. Графическое изображение модельного временного ряда
с линейным трендом
6) Средняя ошибка аппроксимации 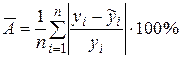 построенной модели составляет 12,9%. Таким образом, точность модели является удовлетворительной.
построенной модели составляет 12,9%. Таким образом, точность модели является удовлетворительной.
Реализация с помощью ППП Excel
Анализ структуры временного ряда, подбор линии тренда и прогнозирование удобно осуществлять с помощью «Пакета анализа» табличного процессора Excel. Отчасти это уже делалось в изложенных выше примерах.
Методику применения ППП Excel проиллюстрируем также на примере следующей задачи (при этом будем опираться на статистические данные, находящиеся в таблице 6.15, и исходить из того, что число наблюдений 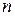 равно 20).
равно 20).
Задача. Для осуществления прогноза исследовать совокупность квартальных данных о динамике выпуска продукции некоторого предприятия за пять лет.
Требуется:
1) ввести данные;
2) проверить гипотезу о существовании тренда с помощью метода сравнения средних уровней;
3) рассчитать значения коэффициентов автокорреляции 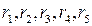 для характеристики структуры временного ряда;
для характеристики структуры временного ряда;
4) построить коррелограмму и с помощью автокорреляционной функции провести анализ структуры временного ряда;
5) провести аналитическое выравнивание временного ряда с использованием линейной, степенной, логарифмической, экспоненциальной и полиномиальной функций;
6) выбрать наилучшую форму тренда по максимальному значению коэффициента детерминации построенных моделей;
7) рассчитать по выбранной наилучшей форме тренда точечный прогноз выпуска продукции во втором квартале шестого года (с учетом сезонных колебаний, если они имеются во временном ряду).
Результаты вычислений и анализа оформить в виде отчета (форма отчета прилагается ниже).
 2015-01-21
2015-01-21 13833
13833
