Пример 7.1. Дана расширенная модель формирования спроса и предложения:
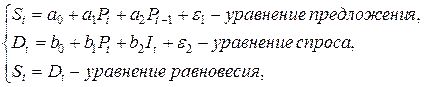
где 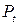 – цена,
– цена, 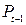 – цена в предыдущий момент времени,
– цена в предыдущий момент времени, 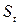 – предложение товара,
– предложение товара, 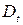 – спрос на товар,
– спрос на товар, 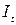 – доход.
– доход.
Составить структурную и приведенную формы модели.
Решение:
Учитывая уравнение равновесия, перейдем от расширенной формы модели к модели:
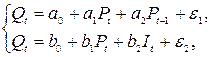
где 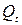 – количество товара (производимого и потребляемого).
– количество товара (производимого и потребляемого).
В данной модели эндогенными переменными (т.е. определяемыми внутри модели) являются переменные 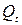 и
и 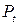 .
.
Предопределенными переменными являются экзогенная переменная 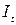 и лаговая эндогенная переменная
и лаговая эндогенная переменная 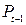 .
.
Поэтому структурная форма модели имеет вид:
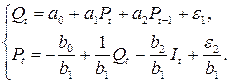
Приведенная форма содержит два уравнения (по числу эндогенных переменных модели). Каждое уравнение приведенной формы представляет собой зависимость эндогенной переменной от предопределенных переменных модели (дохода и цены в предыдущий период). В результате имеем приведенную форму:
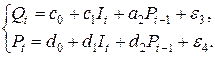
Пример 7.2. Идентифицировать каждое уравнение системы и саму систему в целом
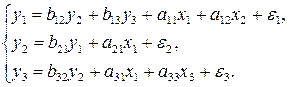
Решение:
Для первого уравнения 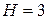 ,
, 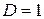 . Так как
. Так как 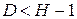 , то ввиду необходимого и достаточного условия (таблица 7.1) уравнение является неидентифицируемым.
, то ввиду необходимого и достаточного условия (таблица 7.1) уравнение является неидентифицируемым.
Для второго уравнения 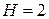 ,
, 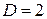 , т.е. выполняется неравенство
, т.е. выполняется неравенство 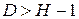 .
.
Кроме того, ранг матрицы, составленной из коэффициентов первого и третьего уравнений при переменных (эндогенных и экзогенных), отсутствующих во втором уравнении, равен двум. Следовательно, на основании необходимого и достаточного условия (таблица 7.1) второе уравнение сверхидентифицируемо.
Для третьего уравнения 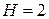 ,
, 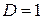 , т.е. выполняется равенство
, т.е. выполняется равенство 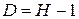 .
.
Кроме того, ранг матрицы, составленной из коэффициентов первого и второго уравнений при переменных (эндогенных и экзогенных), отсутствующих в третьем уравнении, равен двум. Следовательно, на основании необходимого и достаточного условия (таблица 7.1) третье уравнение идентифицируемо.
Так как первое уравнение в системе не идентифицируемо, то вся модель является неидентифицируемой.
Пример 7.3. Идентифицировать следующую структурную модель:
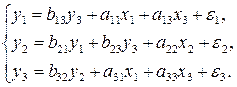

Исходя из приведенной формы модели
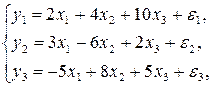
найти структурные коэффициенты.
Решение:
Модель имеет три эндогенные 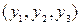 и три экзогенные
и три экзогенные 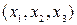 переменные.
переменные.
Проверим для каждого уравнения структурной модели выполнимость необходимого и достаточного условия идентификации, приведенного в таблице (7.1).
Первое уравнение содержит две эндогенные переменные 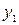 и
и 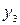 ; в нем отсутствует одна экзогенная переменная
; в нем отсутствует одна экзогенная переменная 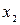 . Значит,
. Значит, 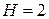 ,
, 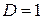 и выполняется равенство
и выполняется равенство 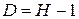 .
.
Построим матрицу 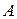 из коэффициентов при переменных
из коэффициентов при переменных 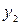 и
и 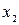 во втором и третьем уравнениях системы:
во втором и третьем уравнениях системы: 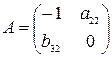 . Так как
. Так как 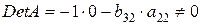 , то ранг матрицы равен 2.
, то ранг матрицы равен 2.
Следовательно, на основании необходимого и достаточного условия (таблица 7.1) первое уравнение идентифицируемо.
Второе уравнение содержит три эндогенные переменные 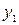 ,
, 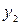 и
и 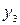 ; в нем отсутствуют две экзогенные переменные
; в нем отсутствуют две экзогенные переменные 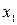 и
и 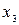 . Значит,
. Значит, 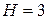 ,
, 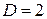 и выполняется равенство
и выполняется равенство 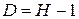 .
.
Построим матрицу 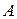 из коэффициентов при переменных
из коэффициентов при переменных 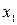 и
и 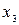 в первом и третьем уравнениях системы:
в первом и третьем уравнениях системы: 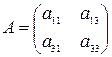 . Так как
. Так как 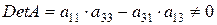 , то ранг матрицы равен 2.
, то ранг матрицы равен 2.
Следовательно, на основании необходимого и достаточного условия (таблица 7.1) второе уравнение идентифицируемо.
Третье уравнение содержит две эндогенные переменные 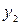 и
и 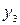 ; в нем отсутствует одна экзогенная переменная
; в нем отсутствует одна экзогенная переменная 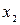 . Значит,
. Значит, 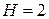 ,
, 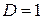 и выполняется равенство
и выполняется равенство 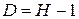 .
.
Построим матрицу 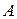 из коэффициентов при переменные
из коэффициентов при переменные 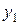 и
и 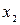 в первом и втором уравнениях системы:
в первом и втором уравнениях системы: 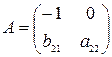 . Так как
. Так как 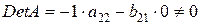 , то ранг матрицы равен 2.
, то ранг матрицы равен 2.
Следовательно, на основании необходимого и достаточного условия (таблица 7.1) третье уравнение идентифицируемо.
Таким образом, исследуемая система идентифицируема. Поэтому для ее решения применим косвенный метод наименьших квадратов: структурные коэффициенты модели с помощью алгебраических преобразований выразим через приведенные коэффициенты.
1. Из третьего уравнения приведенной формы выразим 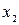 (так как его нет в первом уравнении структурной формы):
(так как его нет в первом уравнении структурной формы):
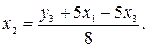
Данное выражение содержит переменные 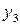 ,
, 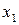 и
и 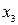 , которые нужны для первого уравнения структурной формы модели. Подставим полученное выражение
, которые нужны для первого уравнения структурной формы модели. Подставим полученное выражение 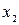 в первое уравнение приведенной формы модели:
в первое уравнение приведенной формы модели:
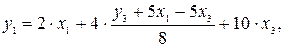
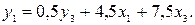
Получили первое уравнение структурной формы модели.
2. Во втором уравнении структурной формы модели нет переменных 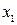 и
и 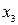 . Параметры второго уравнения структурной формы определим в два этапа.
. Параметры второго уравнения структурной формы определим в два этапа.
На первом этапе выразим 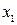
 из первого уравнения приведенной формы модели:
из первого уравнения приведенной формы модели:
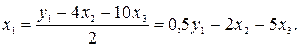
Кроме того, выразим 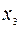 из третьего уравнения приведенной формы модели:
из третьего уравнения приведенной формы модели:
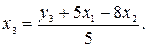
Подставим значение 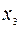 в выражение для
в выражение для 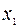 :
:
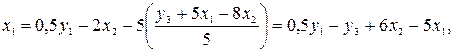
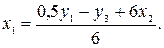
На втором этапе аналогично в выражение для 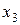 подставим значение
подставим значение 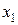 , полученное из первого уравнения приведенной формы модели:
, полученное из первого уравнения приведенной формы модели:
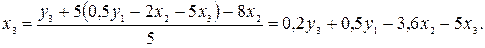
Следовательно, 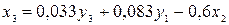 .
.
Подставим теперь полученные значения 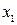 и
и 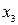 во второе уравнение приведенной формы модели:
во второе уравнение приведенной формы модели:
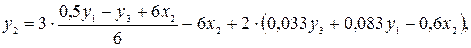
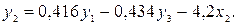
Получили второе уравнение структурной формы модели.
3. Из второго уравнения приведенной формы модели выразим 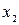 :
:
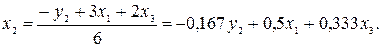
Подставим полученное выражение в третье уравнение приведенной формы модели:
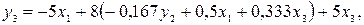
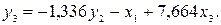
Получили третье уравнение структурной формы модели.
Таким образом, структурная форма модели имеет вид:
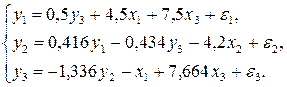
Пример 7.4. Идентифицировать следующую структурную модель:
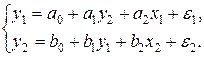
На основании статистических данных, представленных в таблице 7.2, с помощью двухшагового метода наименьших квадратов найти структурные коэффициенты модели.
Таблица 7.2. Статистические данные примера 7.4
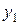 | 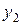 | 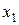 | 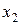 |
| 3,1 | 7,4 | 6,8 | 46,7 |
| 22,8 | 30,4 | 22,4 | 3,1 |
| 7,8 | 1,3 | 17,3 | 22,8 |
| 21,4 | 8,7 | 12,0 | 7,8 |
| 17,8 | 25,8 | 5,9 | 21,4 |
| 37,2 | 8,6 | 44,7 | 17,8 |
| 35,7 | 30,0 | 23,1 | 37,2 |
| 46,6 | 31,4 | 51,2 | 35,7 |
| 56,0 | 39,1 | 32,3 | 46,6 |
Решение:
Проверим уравнения структурной модели на идентифицируемость. Модель имеет две эндогенные 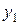 и
и 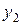 и две экзогенные
и две экзогенные 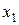 и
и 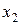 переменные.
переменные.
Первое уравнение содержит две эндогенные переменные 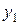 и
и 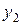 ; в нем отсутствует одна экзогенная переменная
; в нем отсутствует одна экзогенная переменная 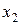 . Значит,
. Значит, 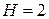 ,
, 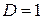 и выполняется равенство
и выполняется равенство 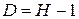 .
.
Построим матрицу 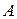 из коэффициентов при переменной
из коэффициентов при переменной 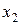 во втором уравнении системы:
во втором уравнении системы: 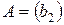 . Так как
. Так как 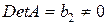 , то ранг матрицы
, то ранг матрицы 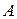 равен 1.
равен 1.
Следовательно, на основании необходимого и достаточного условия (таблица 7.1) первое уравнение системы идентифицируемо.
Второе уравнение содержит две эндогенные переменные 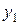 и
и 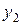 ; в нем отсутствует одна экзогенная переменная
; в нем отсутствует одна экзогенная переменная 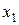 . Значит,
. Значит, 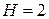 ,
, 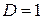 и выполняется равенство
и выполняется равенство 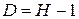 .
.
Построим матрицу 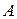 из коэффициентов при переменной
из коэффициентов при переменной 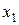 в первом уравнении системы:
в первом уравнении системы: 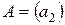 . Так как
. Так как 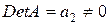 , то ранг матрицы
, то ранг матрицы 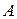 равен 1.
равен 1.
Следовательно, на основании необходимого и достаточного условия (таблица 7.1) второе уравнение системы идентифицируемо.
Таким образом, исследуемая система является идентифицируемой.
Приведенная форма модели имеет вид:
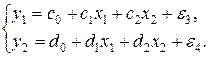
Приведенные коэффициенты вычислим обычным МНК с помощью
инструмента «Регрессия» табличного процессора Excel (используя статистические данные таблицы 7.2):
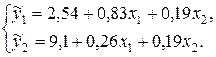
На основе уравнения 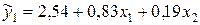 найдем теоретические значения для эндогенной переменной
найдем теоретические значения для эндогенной переменной 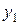 . Для этого подставим в уравнение значения переменных
. Для этого подставим в уравнение значения переменных 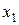 и
и 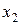 . Аналогично на основе уравнения регрессии
. Аналогично на основе уравнения регрессии 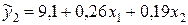 найдем теоретические оценки для эндогенной переменной
найдем теоретические оценки для эндогенной переменной 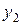 . Результаты вычислений сведем в таблицу 7.3.
. Результаты вычислений сведем в таблицу 7.3.
Таблица 7.3. Теоретические значения переменных 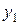 и
и 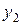
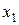 | 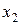 | 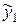 | 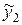 |
| 6,8 | 46,7 | 17,2 | 19,6 |
| 22,4 | 3,1 | 21,8 | 15,5 |
| 17,3 | 22,8 | 21,3 | 17,9 |
| 12,0 | 7,8 | 14,0 | 13,7 |
| 5,9 | 21,4 | 11,6 | 14,7 |
| 44,7 | 17,8 | 43,2 | 24,0 |
| 23,1 | 37,2 | 28,9 | 22,1 |
| 51,2 | 35,7 | 52,0 | 29,1 |
| 32,3 | 46,6 | 38,4 | 26,2 |
Наконец, используя статистические данные таблицы 7.3, с помощью инструмента «Регрессия» обычным МНК вычислим структурные коэффициенты.
В результате структурная форма модели имеет вид:
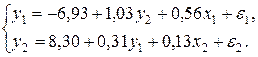
 2015-01-21
2015-01-21 1834
1834
