Mетод состоит в том, что приближение корня ищется как координата точки пересечения касательной с осью О x, проведенной к кривой 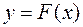 в точке
в точке 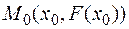 . При этом начальное приближение
. При этом начальное приближение 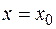 не требует определения отрезка
не требует определения отрезка 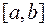 .
.
Уравнение касательной, проходящей через заданную точку к кривой имеет вид:
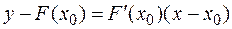 (3)
(3)
Тогда следующее приближение корня определяется как точка пересечения этой касательной с осью абсцисс:
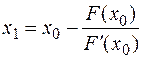 , аналогично для n+1 –го приближения получим
, аналогично для n+1 –го приближения получим 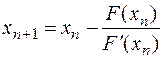 (4), где
(4), где 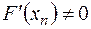 .
.
В формуле (4) 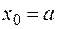 , если
, если 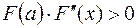 ;
; 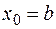 , если
, если 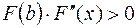 на
на 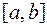 .
.
Для окончания итерационного процесса используется либо условие 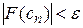 либо условие
либо условие 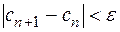 .
.
Пример. Отделить корни аналитически и уточнить их методом касательных с точностью до 0,001.
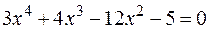
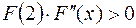 , следовательно, для вычислений применяем формулу
, следовательно, для вычислений применяем формулу 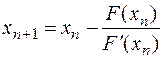 , где
, где 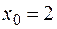 . Вторая производная
. Вторая производная 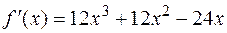
Вычисления представлены в таблице.
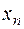
| 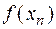
| 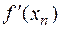
| 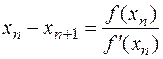
|
| 2,0000 | 27,0000 | 0,28125 | |
| 1,7188 | 6,0404 | 55,12756 | 0,10957 |
| 1,6092 | 0,7100 | 42,456 | 0,01672 |
| 1,5925 | 0,0150 | 40,6721 | 0,00037 |
| 1,5921 | 0,0000 | 40,63327 | 1,8E-07 |
Данные вычислений показывают, что разница между корнями 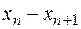 достигает требуемой точности на четвертой итерации. Таким образом, получен корень
достигает требуемой точности на четвертой итерации. Таким образом, получен корень 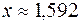 .
.
 2015-01-21
2015-01-21 548
548








