Основные системы компьютерной алгебры

Интегрированные системы символьной математики (компьютерной алгебры) - одно из важных современных направлений в применении компьютеров.

Если традиционное использование последних - манипуляция с числами, то в системах аналитических вычислений компьютер оперирует с выражениями, их преобразованием по определенным заданным правилам, подстановкой одних выражений в другие.

Специфику этих систем проще всего увидеть на вычислении производной.

Пусть, например, вычисляется производная от функции х 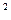. Численной системе нужно задать значение х и для этого значения вычислить функцию, затем задаться малой (но не бесконечно малой) величиной dx и вычислить новое значение функции в точке х+dx, после чего отношение даст приблизительное значение производной в заданной точке. Здесь работа идет только с числами.

Аналитическая система имеет формулу f = х 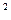и знает правила дифференцирования. Поэтому в качестве производной она выдаст функцию и не потребует численного значения аргумента. Естественно, что для вычисления производной можно задать и несравненно более сложную функцию - производная будет вычислена в соответствии с правилами Лейбница.

Другим ярким примером является вычисление 100!. Аналитические системы выдают точное число длиной более 150 цифр. Числовые системы выдают приблизительное число с плавающей точкой в виде мантиссы и показателя степени.

Основа подхода к аналитическим системам была заложена в 1960-м году Джоном Маккарти, разработавшим язык списков Лисп. Главным объектом в Лиспе является элемент, точнее - его имя. Главной операцией в Лиспе является подстановка.

Эти свойства вскоре привели к построению на базе Лиспа простейших систем работы с формулами. Наиболее известной такой системой был R-Lisp, в котором можно было работать с полиномами, приводить подобные члены, делить полиномы, находить остаток. Вершиной развития R-Lisp’а стал язык Reduce.

Большую известность получили также три класса таких систем: Derive [10,11], свободно оперировавшая производными, но в отличие от Reduce, с элементами графического представления результатов, одна из самых мощных и поныне привлекательных систем Maple V (ядро написано на языке С и система Mathematica. Позже на базе ядра системы Maple V символьные вычисления были реализованы в популярной числовой системе MathCAD, имеющей великолепный пользовательский интерфейс.

Большой популярностью в среде радиоэлектроников получила система Матричная Лаборатория MathLab, в которой заложены средства для обработки сигналов.

Кроме того, создаются большие специализированные системы для различных областей исследований, например, по теории групп (см., в частности, GAP, https://www.exponenta.ru/soft/others/gap/asp) или полиномиальной алгебре (система SINGULAR, https://www.singular. uni-kl.de/).

Reduce

Развитие систем аналитических вычислений стимулировалось не только здоровой любознательностью. Одним из главных стимуляторов, требовавших развития таких систем являлась теоретическая физика. По крайней мере, две области остро нуждались в таком инструменте - это физика элементарных частиц, где требовалось расписание, приведение к стандартному виду и интегрирование большого числа диаграмм Фейнмана, и общая теория относительности, где постановка каждой конкретной задачи требовала расписания метрического тензора, вычисления обратного тензора, вычисления по его производным связностей и по производным последних - тензора кривизны, определяющего уравнения Эйнштейна.

Дальнейшее совершенствование R-Lisp’a в направлении удовлетворения этих запросов привело к созданию в 1968 году A.Hern’ом языка Reduce, основное назначение которого уже была работа с формулами, аналитическое дифференцирование и интегрирование, решение уравнений и систем уравнений.

Для вычислений диаграмм Фейнмана, как внутриязыковые объекты были введены матрицы Дирака и операции работы с ними.

Скачок в развитии аналитических систем произошел с начала 80-х годов с появлением персональных компьютеров. Аналитические системы попали на стол ученого. Исключительную популярность приобрела система Reduce 3.3, написанная A.Hern’ом на базе Лиспа Tsuioshi Yamamoto. Теперь Reduce стал полноценным научным инструментом: в нем можно было проводить и сложнейшие аналитические вычисления, можно было и выражать в числах необходимые величины, и преобразовывать формулы для прямой записи их в программы на Fortran’e.

Однако, следует отметить, что Reduce в конце концов, работает только с текстовой информацией - и формулы и числа вводятся и выводятся только в текстовом виде. Никакого графического интерфейса Reduce не имеет.

Maple

Maple - система символьных вычислений занимает в настоящее время в этой отрасли наряду с системой Mathematica фирмы Wolfram Research ведущие позиции. Она была создана группой символьных вычислений (The Symbolic Group), организованной Кейтом Геддом (Keith Qeddes) и Гастоном Гонэ (Gaston Gonnet) в 1980 году в университете Waterloo, Канада. Система Maple V под Windows (реализации R3, R4 и R5) была реализована на персональных компьютерах фирмой Waterloo Maple Inc. (Канада). Серийная версия Maple V R4 открыто и бесплатно распространяется через Internet, благодаря чему легально попала на многие CD-ROM, свободно распространяемые у нас. Система обладает громадным (свыше 2500) набором самых различных функций для выполнения аналитических и численных вычислений, решения алгебраических и дифференциальных уравнений, графического вывода результатов и многих других действий.