Мажоритарное декодирование. Сущность мажоритарного декодирования излагается в п

Сущность мажоритарного декодирования излагается в п. 2.5.7 на примере линейных кодов.

Поскольку циклический код является разновидностью группового кода, то его проверочные символы должны выражаться через суммы по модулю 2 определенных информационных символов. Основная трудность состоит в нахождении систем контрольных проверок.

Существуют разные способы нахождения системы проверочных равенств. В работе [6], например, для определения проверочных символов используется соотношение

,

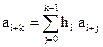где h – двоичные коэффициенты генераторного многочлена 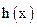, определяемого выражением:

,

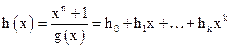где 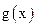– образующий многочлен циклического кода.

Более просто и наглядно данная задача решается, если построить схему деления на сумматорах по модулю 2 и непосредственно по схеме, прослеживая путь прохождения сигнала, составить интересующие соотношения. Рассмотрим этот вопрос на примере кода (7,3) с образующим многочленом 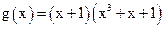. Данный код имеет кодовое расстояние 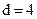, поэтому способен исправлять однократную ошибку и одновременно обнаруживать двойную.

Имеем: .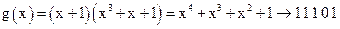

Схема деления на этот образующий многочлен представлена на рис. 2.9.

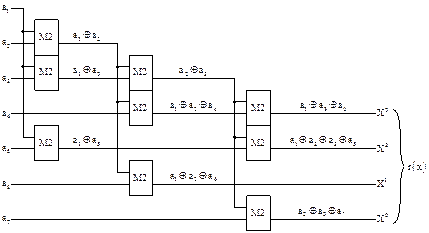
Рис. 2.9. Схема деления на .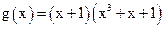

За разрешенные кодовые комбинации циклического кода принимают комбинации, которые делятся без остатка на образующий многочлен. Для рассматриваемого кода это будет иметь место только при выполнении следующих четырех условий:

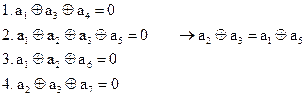
Используя полученные соотношения, выразим 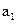через различные символы. Добавляя тривиальную проверку 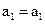, получает систему раздельных проверок для :

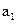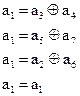
Проверочные равенства для остальных символов в циклических кодах находятся по следующему правилу: каждый последующий символ определяется путем прибавления единицы к номеру предыдущего символа. Номер последнего символа при прибавлении к нему единицы заменяется на единицу.

Используя сформулированное правило, находим проверочные равенства для 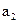и :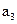

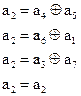
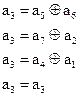
Пример.

Закодировать циклическим кодом (7,3) с 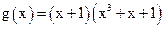безизбыточную комбинацию 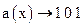и выполнить мажоритарное декодирование при появлении однократной и двойной ошибки.

Решение.

Находим разрешенный КВ:

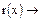Итак,

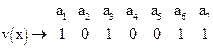
Легко видеть, что при отсутствии искажений все равенства разработанной системы проверок выполняются.

Пусть при передаче произошло искажение 3-го разряда, т.е.

Выполняем проверку:

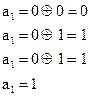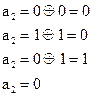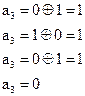Решение принято: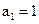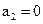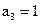

Итак, однократная ошибка исправлена.

Предположим, что произошло искажение 1-го и 5-го разрядов, т.е.

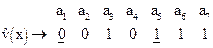
Выполняем проверку:

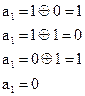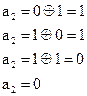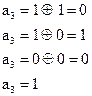Решение не принимается: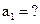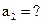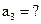

Двойная ошибка фиксируется по равенству 1 и 0 в системе проверочных равенств, при этом не имеет значения как ошибки распределены по КВ. Однако следует иметь в виду, что при двойной ошибке по одному из символов решение принимается, если ошибочные разряды вошли в одну из проверок этого символа. Например, если бы искажение произошло в 1 и 6 разрядах, то решение по 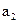было бы принято. Отсюда следует, что, по крайней мере, два мажоритарных элемента должны фиксировать двойную ошибку, т.е. равенство 1 и 0 в системе проверок.