Цепной код

Цепной код относится к группе непрерывных кодов, где операции кодирования и декодирования производятся непрерывно над последовательностью символов без деления ее на блоки.

В цепном коде после каждого информационного элемента следует проверочный элемент, формируемый путем сложения по модулю 2 двух информационных элементов, отстоящих друг от друга на шаг сложения 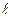. Шаг 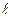– это расстояние между двумя информационными элементами, формирующими проверочный элемент.

Обозначим через 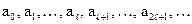информационную последовательность символов. Проверочные символы обозначим через b. Согласно сказанному выше, имеем: ; ; …; ; …

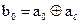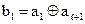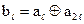Закодированная цепным кодом последовательность имеет вид:

.

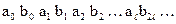Процесс декодирования цепного кода состоит в следующем:

- из поступающей последовательности элементов выделяют отдельно информационные элементы и отдельно проверочные элементы;

- из принятой последовательности информационных элементов по известному правилу кодирования формируются новые проверочные элементы;

- каждый сформированный проверочный элемент складывается по модулю 2 с принятым проверочным элементом. При отсутствии искажений результатом суммирования будет 0, в противном случае – 1.

В теории кодирования доказывается, что при шаге сложения 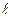цепной код способен исправлять пачки ошибок длиной 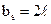. Изменяя шаг сложения, можно согласовывать корректирующие способности кода с характеристиками канала связи.

Простейшим цепным кодом является код Финка-Хагельбергера, имеющий 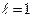, т.е. 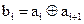. Этот код позволяет исправлять все одиночные ошибки при условии, что между двумя любыми ошибочно принятыми символами имеется по крайней мере три правильно принятых символа. Рассмотрим пример.

Предположим, что в последовательности символов кода Финка-Хагельбергера 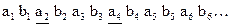подверглись искажению символы 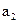и .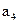

Исправление ошибок осуществляется в следующей последовательности:

– с момента обнаружения ошибки регистрируются все неправильные проверки до появления правильной. Имеем:

1)

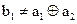
2)

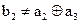
3)

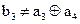
4)

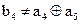
5) 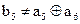. 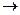Вывод: 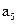– достоверно.

– в проверке 4) 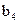– достоверно, т.к. в противном случае в проверке 3) было бы равенство (между двумя ошибочными символами должно быть не менее трех правильных символов). Вывод: искажен символ 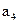, следовательно, 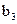, 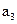и 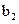– достоверны;

– в проверке 2) искаженным является символ 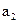, т.к. при искажении 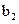выполнялась бы проверка 1).