Интенсивностью распределенной нагрузки

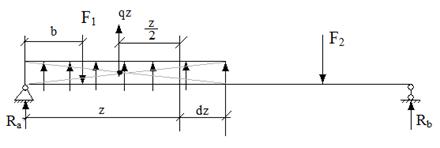
Рассмотрим балку, нагруженную произвольной нагрузкой. Определим поперечную силу в сечении, стоящем от левой опоры на расстоянии 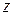. Спроецировав на вертикаль все силы, расположенные левее сечения, получим:

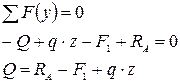
Аналогично вычислим поперечную силу в смежном сечении, расположенном на расстоянии 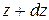от левой опоры:

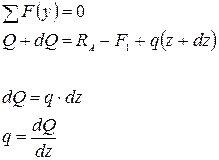
Производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Вычислим теперь изгибающий момент в сечении с абсциссой 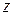, взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длиной 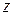заменим ее равнодействующей, равной 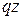и приложенной в середине участка, на расстоянии 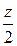от сечения:

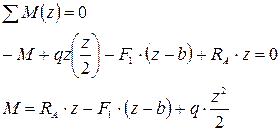
Аналогично вычислим изгибающий момент в смежном сечении, стоящем от левой опоры на расстоянии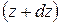

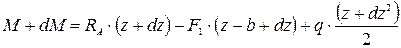(2)

Вычитая из (1) – (2), получим:

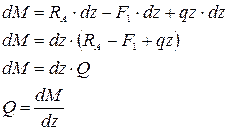
т.е. производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).

Взяв производную от обеих частей равенства, получим:

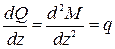
т.е. вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Все полученные зависимости будем использовать в дальнейшем главным образом при построении эпюр поперечных сил и изгибающих моментов.