Найдем потенциал диполя (Рис. 28)в точке A 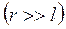 .
.
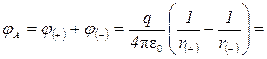
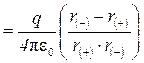
Так как 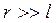 , то
, то 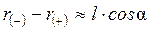 ,
, 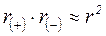 (
(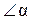 — угол между направлением момента диполя
— угол между направлением момента диполя 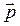 и радиусом вектором
и радиусом вектором 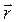 , проведенным от диполя к «точке наблюдения» A).
, проведенным от диполя к «точке наблюдения» A).
Проведем  от любой точки диполя ввиду малого
от любой точки диполя ввиду малого  .
.
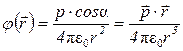
Поле зависит от 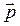 и убывает с расстоянием пропорционально
и убывает с расстоянием пропорционально 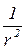 (быстрее поля точечного заряда).
(быстрее поля точечного заряда).
| Рис. 29 |
Для нахождения поля диполя, вычислим проекции 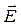 на два взаимно перпендикулярных направления ортов
на два взаимно перпендикулярных направления ортов 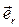 и
и 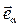 (Рис. 29).
(Рис. 29).
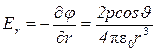
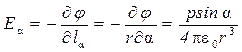
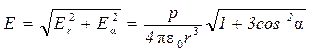
При 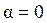 :
: 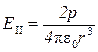 — поле на оси диполя.
— поле на оси диполя.
При 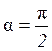 :
: 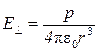 — поле перпендикулярно направлению оси.
— поле перпендикулярно направлению оси.
Напряженность поля диполя убывает пропорционально 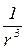 , быстрее напряженности поля точечного заряда.
, быстрее напряженности поля точечного заряда.
Рассмотрим поведение диполя в электростатическом поле.
1) Однородное поле 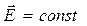
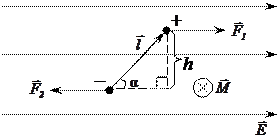 Рис. 30 Рис. 30 |
На концы диполя действуют равные по модулю противоположно-направленные силы (пара сил) (Рис. 30):
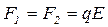
Момент пары сил
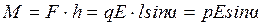
следовательно, 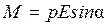 ,
, 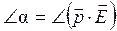 , а значит
, а значит
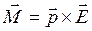 .
.
Однородное электрическое поле стремится развернуть диполь так, чтобы электрический момент диполя 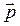 был направлен по полю
был направлен по полю 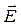 .
.
Из анализа выражения для 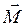 видно, что существует два положения равновесия диполя в однородном поле (Рис. 31):
видно, что существует два положения равновесия диполя в однородном поле (Рис. 31):
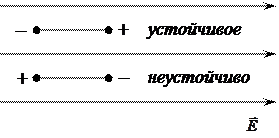 Рис. 31 Рис. 31 |
а) 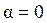 ,
, 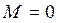 — устойчивое равновесие
— устойчивое равновесие 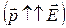
б)  ,
, 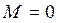 — неустойчивое равновесие
— неустойчивое равновесие 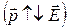
| Рис. 32 |
2) Неоднородное поле.
Результирующая сила, действующая на диполь (Рис.32):
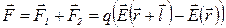
Представим 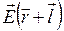 в виде ряда по
в виде ряда по  ,
, 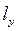 ,
, 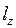 и ограничимся линейными членами:
и ограничимся линейными членами:
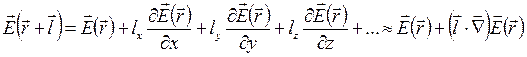
где 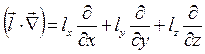 .
.
Следовательно 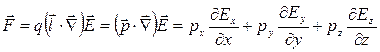
Сила 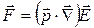 направлена по
направлена по  ,
,
где 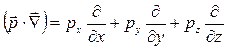 — дифференциальный оператор.
— дифференциальный оператор.
То есть на диполь, помещенный в неоднородное поле, действует сила, втягивающая диполь в область сильного поля и пара сил 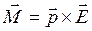 , стремящаяся повернуть диполь параллельно полю.
, стремящаяся повернуть диполь параллельно полю.
 2015-02-24
2015-02-24 2794
2794
