Электрическое поле диполя Герца

Электрическое поле можно вычислить двумя способами: непосредственно из уравнений Максвелла, по известному магнитному полю, либо используя соотношение:

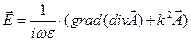. (3.3.1)

Пусть среда распространения волн – воздух. Тогда 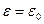. Для вычисления div воспользуемся декартовой системой координат: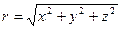

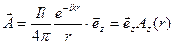
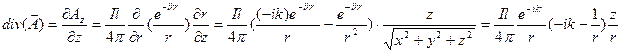
Представим 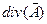в сферической системе координат учитывая, что :

.

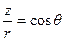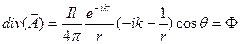Вычислим gradФ:

.

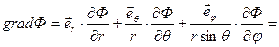
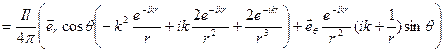Теперь, подставляя полученное выражение в формулу 3.3.1. запишем окончательно электрическое поле диполя Герца:

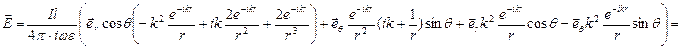
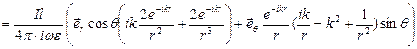
В полученном выражении можно выделить две компоненты: .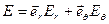

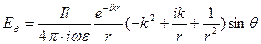
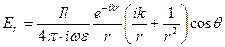
Выводы:

1) Электрическое поле диполя Герца имеет радиальную (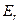) и угломестную (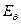) составляющие, причем радиальная компонента убывает значительно быстрее угломестной.

2) В зависимости от расстояния от диполя до точки наблюдения можно сделать разделение по трем зонам: (а) ближняя, (б) промежуточная, (в) дальняя. Под ближней зоной подразумевают область, где наибольшую амплитуду имеет компонента с 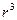в знаменателе. В дальней зоне, где электрическое поле имеет только угломестную компоненту, наибольшая амплитуда будет у компоненты с 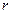в знаменателе.

.

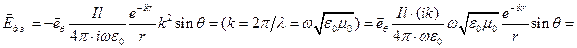
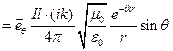Теперь, учитывая, что величина 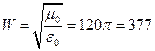Ом - импеданс свободного пространства, запишем окончательное выражения для электрического поля диполя Герца в дальней зоне:

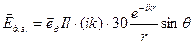. (3.3.2.)