Векторный потенциал диполя Герца

Элементарный электрический вибратор.

Диполь Герца – это элементарный линейный излучатель, длина которого много меньше длины волны с постоянным распределением тока по его длине.

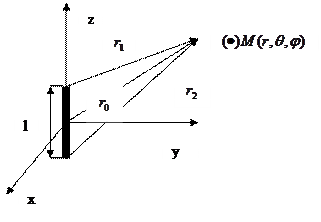
Рис. 3.1 Диполь Герца в декартовой системе координат

Диполь Герца представляет собой идеализированный объект. На практике применение таких коротких антенн неэффективно, ввиду плохих полевых характеристик, кроме того, у реальных антенн распределение тока по длине не может быть постоянным. Вместе с тем, поле излучение диполя Герца весьма просто описывается математически, поэтому его можно использовать как элементарный объект, полезный для описания более сложных линейных антенн. Например, в антенне типа «волновой канал» (рис.3.2) можно представить все токопроводящие элементы как суперпозицию электрических диполей Герца.

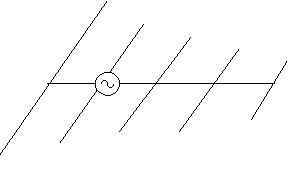
Рис. 3.2 Антенна «волновой канал»

Далее суммарное поле в точке наблюдения от всех элементарных диполей позволит вычислить поле излучения всей антенны. Таким образом, зная распределение тока по антенне, мы сможем достаточно просто описать полевые характеристики сложной линейной антенны.

Кроме того, режим работы антенны, близкий к режиму диполя Герца имеет место в тех устройствах, в которых стараются любой ценой минимизировать линейные размеры (например, в антеннах мобильных телефонов или антеннах диапазонов ДВ и СДВ).

Найдем векторный потенциал диполя Герца в произвольной точке пространства:

,

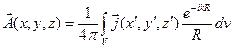где 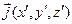известно и удовлетворяет данному ранее определению.

Поместим диполь Герца в центр сферической системы координат.

,

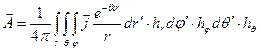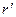
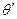
где 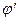- координаты точки интегрирования.

При интегрировании 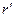будет меняться от 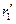до 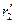, но так как длина диполя Герца мала, то можно сделать приближение следующего вида: 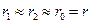, где 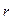- расстояние от центра координат до точки наблюдения, поэтому мы можем вынести функцию Грина из интеграла:

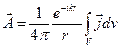
Представляя элементарный объем в виде 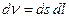, и учитывая, что 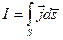- полный ток, получим:

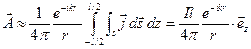(3.1)