Рассмотрим простейшую цепь переменного тока из двух параллельных ветвей, как систему, в которой возникают вынужденные электромагнитные колебания под действием источника внешнего напряжения (рис.161).
Рассчитать силу тока и сдвиг фаз между током в цепи и напряжением источника можно по формулам: 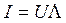 ,
, 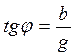 ,
,
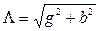 ,
, 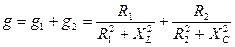 ,
, 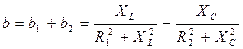 .
.
Анализ этих формул показывает, что так как активная и реактивная проводимости зависят от частоты, то и сила тока во всей цепи также зависит от частоты. 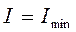 при b=0. Найдем частоту, при которой амплитуда тока минимальна:
при b=0. Найдем частоту, при которой амплитуда тока минимальна:
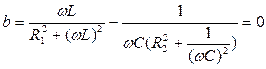 ,
, 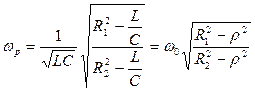 .
.
Это выражение имеет действительное значение при: 1) 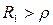 и
и 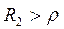 или 2)
или 2) 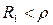 и
и  . Если
. Если 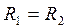 , то амплитуда силы тока минимальна при
, то амплитуда силы тока минимальна при 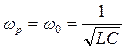 .
.
В этом случае активные и реактивные проводимости равны, сдвиг фаз между током и напряжением равен нулю. Кроме того равны активные и реактивные составляющие токов и токи в ветвях. Поэтому это соотношение параметров в ветвях цепи называют «резонанс токов».
При резонансе токов суммарная реактивная мощность цепи равна нулю: 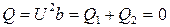 , реактивные мощности
, реактивные мощности 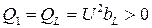 и
и 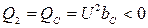 . В этом случае цепь обладает только активным сопротивлением и в цепи выделяется только активная мощность.
. В этом случае цепь обладает только активным сопротивлением и в цепи выделяется только активная мощность.
Резонанс токов возникает и в цепи, содержащей несколько ветвей с активным сопротивлением, емкостями и индуктивностями при том же условии – реактивная проводимость всей цепи равна 0.
 2015-02-24
2015-02-24 874
874







