2015-02-24
237
2.1. Уравнения вида
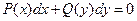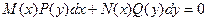, или 
, или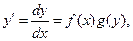 
называются уравнениями с разделяющимися переменными.
2.2. Уравнение вида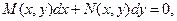 
где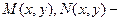 
непрерывные в некоторой области и однородные функции одной и той же степени, называется однородным.
Функция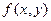 
называется однородной степени m если для любого t выполняется равенство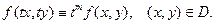 
С помощью замены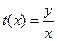 
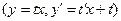однородное уравнение сводится к уравнению с разделяющимися переменным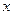и 
и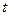 
.
2.3. Уравнение вида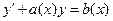 
, линейное относительно неизвестной функции 
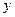, называется неоднородным линейным дифференциальным уравнением первого порядка.
Общее решение линейного уравнения всегда можно записать в виде
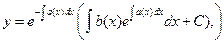, где С – произвольная постоянная.
