Формальное решение задачи (1) строится по известным формулам Крамера:
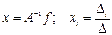
Формальное решение устойчиво, т.е. непрерывно зависит от входных данных A и f.
Действительно, варьируя 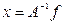 , найдем:
, найдем:
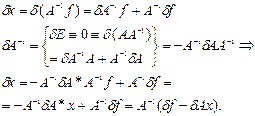
Получаем, что:
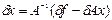 (4)
(4)
Таким образом:
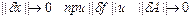
Нормы
Основные используемые в 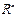 нормы:
нормы:
1) Норма вектора x.
Запишем разложение вектора по базису:
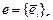
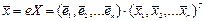 .
.
Базисные вектора образуют строку e, а координаты вектора ` x - столбец X
a) Евклидова норма вектора
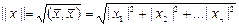
b) 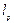 -Норма (при p=2 норма Гильберта - Шмидта)
-Норма (при p=2 норма Гильберта - Шмидта)
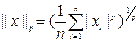
(для конечномерного случая 1/n можно перед суммой опустить).
с) c - норма (равномерная или Чебышевская норма вектора x)
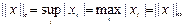
В 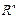 имеют место соотношения:
имеют место соотношения:
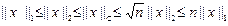
т.е. в 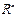 все эти нормы эквивалентны и сходимость в любой из них влечет сходимость в остальных нормах.
все эти нормы эквивалентны и сходимость в любой из них влечет сходимость в остальных нормах.
Проверим, например:
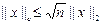
Имеем:
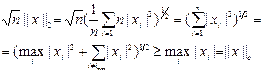
2). Норма матрицы А. Норма матрицы А, согласованная с нормой вектора x определяется следующим образом:
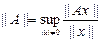
Отсюда 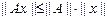
Это условие согласования норм ||x| | и ||A||.
Можно проверить, что введенная таким образом норма матрицы удовлетворяет неравенствам:
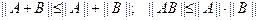 ,
,
Для квадратных матриц 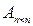 наиболее употребительны следующие нормы:
наиболее употребительны следующие нормы:
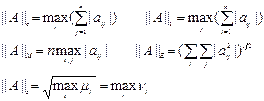
(где 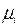 - собственные значения симметричной самосопряженной матрицы
- собственные значения симметричной самосопряженной матрицы 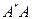 ,
, 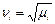 ).
).
Первые две нормы не имеют специальных названий:
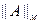 - называется максимальной,
- называется максимальной,
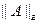 - сферической или евклидовой,
- сферической или евклидовой,
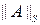 - спектральной.
- спектральной.
Умножая вектор х на матрицу А, получаем новый вектор Ах, норма которого может сильно отличаться от нормы вектора х.
Величину 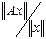 можно рассматривать как своеобразный «коэффициент растяжения» вектора х матрицей А. Для некоторых векторов он может быть малым, а для некоторых большим.
можно рассматривать как своеобразный «коэффициент растяжения» вектора х матрицей А. Для некоторых векторов он может быть малым, а для некоторых большим.
Если M и m – максимальное и минимальное значение коэффициента растяжения, то 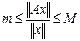
Нормой матрицы А называется максимальное значение коэффициента растяжения:
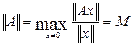
Минимальное значение коэффициента растяжения также играет важную роль в линейной алгебре.
Если А – невырожденная матрица, то для нормы обратной матрицы справедливо равенство:
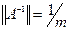
 2015-02-24
2015-02-24 808
808








