Пусть 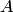 и
и 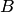 — квадратные матрицы одного и того же порядка. Тогда
— квадратные матрицы одного и того же порядка. Тогда
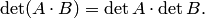
| (2.6) |
т.е. определитель произведения матриц равен произведению их определителей.
Доказательство теоремы проводится в три этапа. Во-первых, теорема справедлива, если один из сомножителей имеет простейший вид (см. рис. 1.6). Пусть, например, матрица 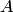 квадратная л-го порядка имеет простейший вид:
квадратная л-го порядка имеет простейший вид: 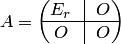 . Если
. Если 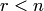 , то в произведении
, то в произведении 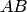 последние
последние 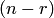 строк будут нулевыми. Тогда по свойствам 1,2 определителей:
строк будут нулевыми. Тогда по свойствам 1,2 определителей: 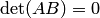 и
и 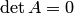 , т.е. равенство (2.6) верно. Если же
, т.е. равенство (2.6) верно. Если же  , то
, то 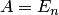 — единичная матрица. Тогда
— единичная матрица. Тогда
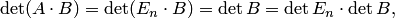
т.е. равенство (2.6) справедливо. Аналогично рассматривается случай, когда матрица 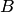 имеет простейший вид.
имеет простейший вид.
Второй этап — доказательство формулы (2.6) для элементарных матриц. Если матрица 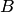 элементарная вида (1.1), (1.3) или (1.5), то ее определитель равен
элементарная вида (1.1), (1.3) или (1.5), то ее определитель равен 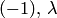 или 1 соответственно, а произведение
или 1 соответственно, а произведение 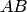 есть элементарное преобразование столбцов матрицы
есть элементарное преобразование столбцов матрицы 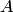 . По свойствам 1, 3, 6 или 9 определителей убеждаемся в справедливости (2.6). Аналогично рассматривается случай, когда матрица
. По свойствам 1, 3, 6 или 9 определителей убеждаемся в справедливости (2.6). Аналогично рассматривается случай, когда матрица 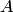 элементарная вида (1.2), (1.4), (1.6).
элементарная вида (1.2), (1.4), (1.6).
Третий этап — доказательство формулы (2.6) для произвольных квадратных матриц n-го порядка. По теореме 1.2 любую квадратную матрицу можно представить в виде произведения простейшей (она является элементарной) и элементарных преобразующих матриц:
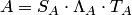 и
и 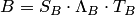 .
.
Тогда, используя результат первых двух этапов, можно записать
что и требовалось доказать.
21. Обернена матриця. Невироджені матриці, критерій невиродженості матриць.
 2015-02-27
2015-02-27 5242
5242
