Основные леммы об определителях

Лемма 1.3 (о разложении по первому столбцу). Определитель равен сумме произведений элементов 1-го столбца на их алгебраические дополнения, т. е.

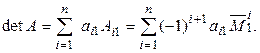
►Доказательство проведем методом математической индукции по размерности определителя.

а) Проверим верность утверждения для n = 2:

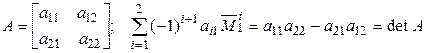–истинно.

б) Предполагая, что утверждение верно для определителей (n – l)-гo порядка, докажем его для определителей n -го порядка.

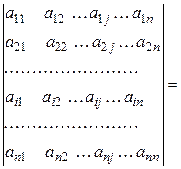[определение или разложение по первой строке] =

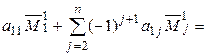= [предположение индукции или разложение по первому столбцу определителя (n – 1)-го порядка ] =

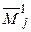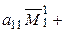
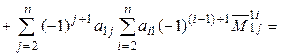
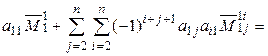
= [лемма 1.1]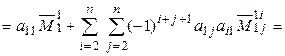

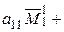
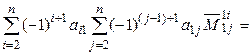
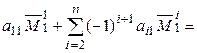
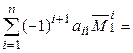
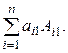
Замечания. 1. При разложении определителя по первой строке все дополнительные миноры 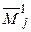, за исключением первого, имеют одинаковый первый столбец, поэтому в разложении первое слагаемое выделяется отдельно.

2. В определителе 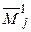элемент 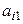находится в строке с номером i− 1.

3. В том, что 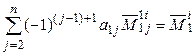, убеждаемся непосредственно, разлагая 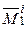по первой строке.◄

Лемма 1.4 (о равноправии строк и столбцов). При транспонировании матрицы ее определитель не меняется, т. е.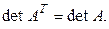

Докажите это утверждение самостоятельно, в качестве упражнения, методом математической индукции по размерности определителя.

После доказательства этой леммы можно утверждать, что все свойства, доказанные для строк определителя, справедливы также и для его столбцов и наоборот.

Лемма 1.5 (о перестановке строк или столбцов). При перестановке в определителе двух строк (столбцов) местами определитель лишь поменяет знак.

►Доказательство проводим для строк определителя в два этапа.

1. Методом математической индукции докажем утверждение для случая, когда меняются местами две соседних строки: i -я и (i + 1)-я.

а) Проверяем утверждение при 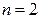. Пусть

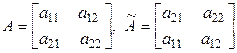Тогда .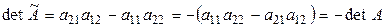

б) Предполагая, что утверждение справедливо для определителей

(n - 1)-го порядка, доказываем его для определителей n -го порядка. Пусть

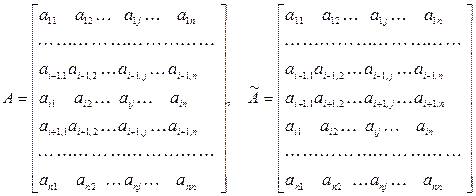Обозначим 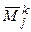– дополнительные миноры к элементу матрицы А, расположенному в k -й строке и j -м столбце, а 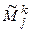– дополнительные миноры к элементу матрицы 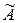, расположенному на том же месте. Нетрудно заметить, что 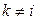при и при 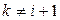миноры 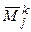и 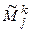отличаются друг от друга лишь тем, что в них две соседние строчки поменялись местами. Итак,

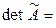[лемма 1.3]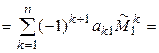 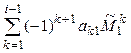+ + 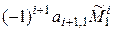+ 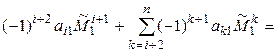[предположение индукции] =

= =

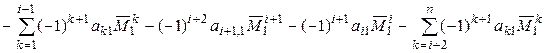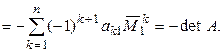2. Поменяем местами строки, которые соседними не являются, например, i -ю и k -ю. Будем обозначать строки матрицы А большими буквами с верхними индексами (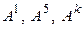 – соответственно 1-я, 5-я и k -я строки матрицы А). Тогда

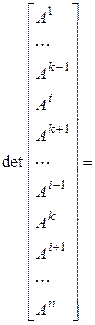
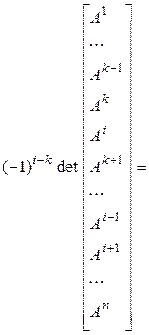
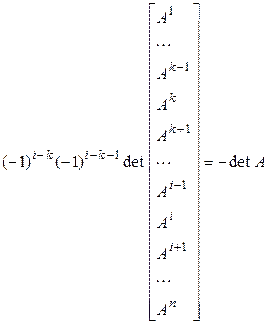
(первое действие – переставляем k -ю строку на ее место, каждый раз меняя ее с соседней, второе – переставляем i -ю строку на ее место, каждый раз меняя ее с соседней).◄

Tеорема 1.1 (основная теорема об определителях). Если в определителе выбрать какую-либо строку (столбец), то определитель равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения, т. е.

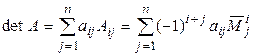– (1.12)

разложение по i -й строке,

–

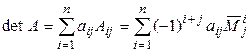разложение по j -му столбцу.

►Доказательство проведем для строк определителя, т. е. докажем формулу (1.12). Обозначим А – исходную матрицу, и 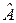– матрицу, полученную из А, если мы в ней переставим i -ю строку на место первой, всякий раз меняя ее с соседней:

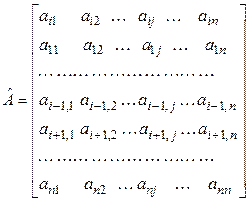Заметим, что если в последней матрице вычеркнуть первую строку и j -й столбец, то получим такой же минор, как если бы в исходной матрице вычеркнули i -ю строку и j -й столбец. Тогда

◄

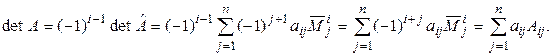Следствие. Определитель треугольной или диагональной матрицы равен произведению её диагональных элементов.

Обобщением теоремы 1.1 является

Теорема 1.2 (Лапласа). Если в определителе выделить 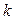строк (столбцов), то определитель равен сумме произведений всех миноров 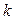-го порядка, расположенных в выделенных строках (столбцах), на их алгебраические дополнения.