2015-07-21
12454
Пример 10. Дана матрица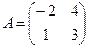 
. Найти обратную матрицу.
Решение.
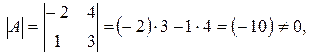
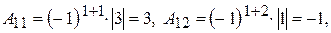
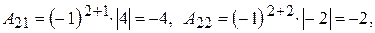
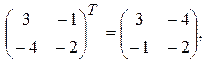
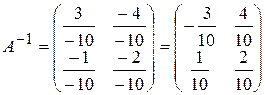
Проверка. Убедимся, что найдена действительно обратная матрица. Найдем произведение матриц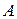 
и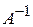 
.
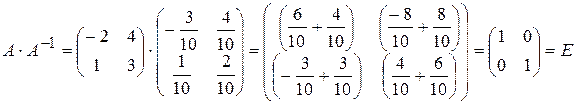
Свойства обратной матрицы
1. 
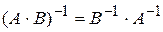, где А и В – невырожденные квадратные матрицы одинакового порядка.
2. 
.
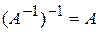3. 
.
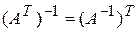4. 
.
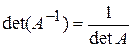Контрольные вопросы
1. Дайте определение матрицы и укажите ее виды.
2. Как проводятся линейные операции над матрицами - сложение матриц, умножение на число?
3. Даны матрицы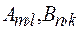 
. При каких условиях на 
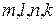определены матрицы 
?
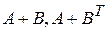4. Как умножить матрицу на матрицу? Запишите условие, которому должны удовлетворять первая и вторая матрицы-сомножители.
5. Как найти любой элемент произведения матриц?
6. Даны матрицы 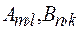. При каких условиях на 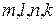определены матрицы 
?
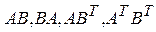7. Запишите свойства суммы и произведения матриц.
8. Какая матрица называется транспонированной к данной? Составьте матрицу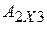 
и транспонируйте ее. Какова ее размерность? Запишите свойства операции транспонирования.
9. Какая матрица называется единичной? Нулевой? Приведите примеры.
10. Запишите элементы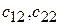 
матрицы 
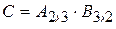и элементы 
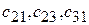матрицы 
.
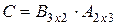11. Что называется определителем второго порядка?
12. Как вычислить определитель третьего порядка?
13. Как вычислить определитель 3 порядка по правилу треугольников?
14. Что называется алгебраическим дополнением элемента определителя? Приведите примеры для определителей 2 и 3 порядков.
15. Напишите разложения определителя третьего порядка по элементам произвольной строки и произвольного столбца.
16. Сформулируйте основные свойства определителей.
17. В каком случае определители равны нулю? Приведите примеры.
18. Представьте определитель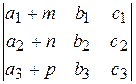 
в виде суммы двух определителей.
19. Заполните пропущенные места так, чтобы значения определителей были одинаковы: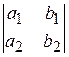 
и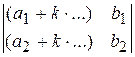 
.
20. Запишите определитель третьего порядка треугольного вида. Как его вычислить?
21. Какая матрица называется обратной для данной матрицы?
22. Для любой ли квадратной матрицы существует обратная?
23. Пусть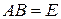 
. Будут ли матрицы 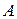и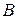 
взаимно обратными?
24. При каких значениях параметра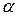 
существует матрица, обратная матрице 
?
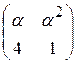25. Запишите формулу для нахождения обратных матриц 2 и 3 порядков.
26. Сформулируйте правило нахождения обратной матрицы.
