1. При изоморфизме линейных пространств 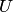 и
и 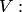
– их нулевые элементы соответствуют друг другу 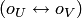 ;
;
– противоположные элементы соответствуют друг другу.
Это следует из определения, если в условии 2 положить 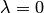 или
или 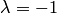 .
.
2. Линейной комбинации векторов пространства 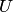 соответствует линейная комбинация соответствующих векторов пространства
соответствует линейная комбинация соответствующих векторов пространства 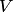 .
.
3. Линейно независимой (линейно зависимой) системе векторов пространства 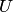 соответствует линейно независимая (линейно зависимая) система векторов пространства
соответствует линейно независимая (линейно зависимая) система векторов пространства 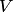 . Действительно, из пунктов 1,2 следует, что равенства
. Действительно, из пунктов 1,2 следует, что равенства 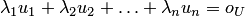 и
и 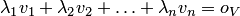 равносильны. Если не все коэффициенты
равносильны. Если не все коэффициенты 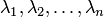 равны нулю, то обе системы
равны нулю, то обе системы 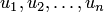 и
и 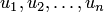 линейно зависимы, в противном случае, обе системы линейно независимы.
линейно зависимы, в противном случае, обе системы линейно независимы.
4. Любое n-мерное линейное вещественное пространство 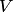 изоморфно n-мерному арифметическому пространству
изоморфно n-мерному арифметическому пространству 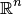 , а л -мерное комплексное пространство изоморфно
, а л -мерное комплексное пространство изоморфно 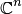 .
.
Это следует из пункта 4 замечаний 8.5, где установлено взаимно однозначное соответствие 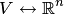 между векторами и координатными столбцами. Линейные операции с векторами в координатной форме показывают, что это взаимно однозначное соответствие является изоморфизмом.
между векторами и координатными столбцами. Линейные операции с векторами в координатной форме показывают, что это взаимно однозначное соответствие является изоморфизмом.
5. Если пространство 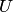 изоморфно пространству
изоморфно пространству 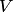 , а
, а 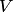 изоморфно пространству
изоморфно пространству 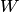 , то пространства
, то пространства 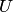 и
и 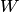 также изоморфны.
также изоморфны.
В самом деле, имея взаимно однозначные соответствия 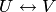 и
и 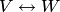 , поставим в соответствие вектору
, поставим в соответствие вектору 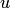 такой вектор
такой вектор 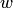 , что
, что 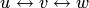 . Такое "сквозное" соответствие
. Такое "сквозное" соответствие 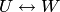 будет взаимно однозначным, сохраняющим линейные операции.
будет взаимно однозначным, сохраняющим линейные операции.
Теорема 8.3 об изоморфизме линейных пространств. Два конечно мерных линейных пространства (над одним и тем же числовым полем) изоморфны тогда и только тогда, когда они имеют одну и ту же размерность.
Действительно, если пространства изоморфны 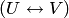 , то базису
, то базису 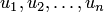 пространства
пространства 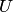 соответствует линейно независимая система векторов
соответствует линейно независимая система векторов 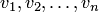 пространства
пространства 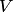 (см. пункт 3 замечаний 8.6), которую в случае необходимости можно дополнить до базиса пространства
(см. пункт 3 замечаний 8.6), которую в случае необходимости можно дополнить до базиса пространства 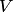 (см. теорему 8.2). Следовательно,
(см. теорему 8.2). Следовательно, 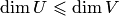 . Аналогично получаем противоположное неравенство
. Аналогично получаем противоположное неравенство 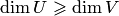 . Таким образом,
. Таким образом, 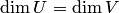 (необходимость доказана). Достаточность следует из пунктов 4,5 замечаний 8.6. Действительно, пусть пространства
(необходимость доказана). Достаточность следует из пунктов 4,5 замечаний 8.6. Действительно, пусть пространства 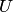 и
и 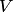 определены над полем
определены над полем 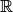 и
и 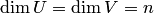 . Тогда, выбрав любые базисы в пространствах
. Тогда, выбрав любые базисы в пространствах 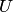 и
и 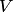 , установим изоморфизмы
, установим изоморфизмы 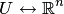 и
и 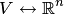 , если
, если 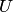 и
и 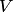 — вещественные пространства. Если пространства
— вещественные пространства. Если пространства 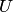 и
и 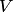 определены над полем
определены над полем 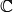 комплексных чисел, то
комплексных чисел, то 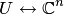 и
и 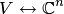 . В обоих случаях, согласно пункту 5 замечаний 8.6, пространства
. В обоих случаях, согласно пункту 5 замечаний 8.6, пространства 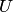 и
и 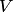 изоморфны. Теорема доказана.
изоморфны. Теорема доказана.
Следствие. Изучение конечномерных линейных пространств сводится к изучению арифметических пространств той же размерности.
45. Матриця переходу від старого базису до нового базису. Координатні стовпці вектора в двох базисах.
Пусть векторы 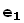 ,...,
,..., 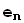 образуют базис пространства V, а векторы
образуют базис пространства V, а векторы 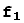 ,
, 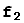 ,...,
,..., 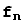 - другой базис этого пространства. Каждый вектор
- другой базис этого пространства. Каждый вектор 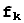 разлагается по базису
разлагается по базису 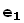 ,...,
,..., 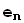 . Запишем эти разложения в виде системы равенств
. Запишем эти разложения в виде системы равенств
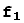 =
= 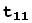
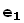 +
+ 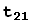
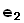 +... +
+... + 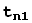
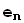 ,
,
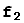 =
= 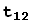
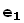 +
+ 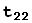
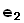 +... +
+... + 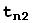
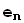 ,
,
............................................
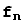 =
= 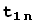
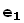 +
+ 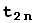
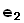 +... +
+... + 
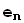 (2)
(2)
или, кратко,
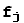 =
= 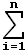
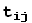
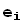
(суммирование по первому индексу коэффициентов 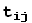 ).
).
Коэффициенты 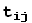 разложений (2) образуют матрицу T перехода от базиса
разложений (2) образуют матрицу T перехода от базиса 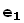 ,...,
,..., 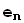 к базису
к базису 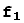 ,
, 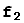 ,...,
,..., 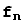 .
.
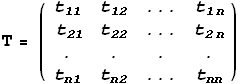
Столбец с номером k матрицы Т состоит из координат базисного вектора 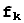 в базисе e.
в базисе e.
Рассмотрим матрицы e = (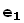 ,...,
,..., 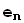 ) и f = (
) и f = (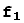 ,
, 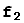 ,...,
,..., 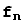 ) размерности 1×n, матричными элементами которых являются старые или новые базисные векторы. Тогда соотношения (2) можно записать с помощью произведения матриц e и T в виде
) размерности 1×n, матричными элементами которых являются старые или новые базисные векторы. Тогда соотношения (2) можно записать с помощью произведения матриц e и T в виде
f = e T (3)
Матрица Т невырождена, и обратная к ней матрица 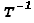 является матрицей перехода от нового базиса f к старому базису e:
является матрицей перехода от нового базиса f к старому базису e:
e = f 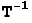
Рассмотрим произвольный вектор v и его разложения по старому и новому базисам
v = 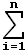
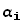
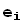 , v =
, v = 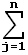
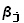
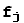 (4)
(4)
Подставляя в правую часть второго из соотношений (4) выражения (2), а в левую часть первое из разложений (4) и приравнивая коэффициенты при базисных векторах 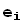 , приходим к следующему выражению координат α через координаты β:
, приходим к следующему выражению координат α через координаты β:
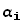 =
= 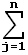
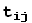
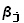 (5)
(5)
Введем матрицу α размерности n×1, матричными элементами которой являются координаты 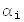 вектора v в старом базисе
вектора v в старом базисе
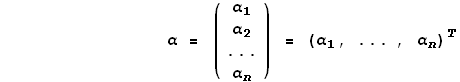
и аналогичную матрицу координат β. Тогда формула (5) может быть записана в виде произведения матриц:
α = T β
46. Підпростори, сума та перетин підпросторів. Теорема Грасмана.
 2015-02-27
2015-02-27 693
693








