2015-02-27
506
1. Понятие прямой суммы распространяется на любое конечное число слагаемых. Сумма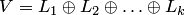 
называется прямой суммой подпространств, если пересечение каждого из них с суммой остальных равно одному нулевому вектору:
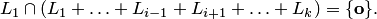
2. Свойства и признаки, указанные для прямой суммы двух подпространств, справедливы и для любого конечного числа слагаемых. Отметим еще одно свойство: если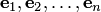 
— базис пространства 
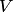, то.
Пример 8.7. В примере 8.6 найдены алгебраические суммы подпространств. Какие суммы являются прямыми?
Решение. Так как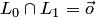 
, то сумма 
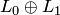— прямая. Аналогично полу чаем, что суммы
— прямые.
Остальные суммы подпространств, найденные в примере 8.6, не являются прямыми:
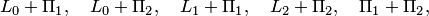
поскольку их пересечение содержит не только нулевой вектор. Например, пересечение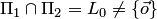 
.
48. Найпростіші задачі аналітичної геометрії.
