Прямая сумма подпространств

Алгебраическая сумма подпространств 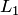и 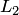линейного пространства 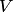называется прямой суммой, если пересечение подпространств состоит из одного нулевого вектора. Прямая сумма подпространств обозначается 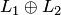и обладает следующим свойством: если 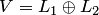, то для каждого вектора 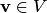существует единственное представление в ви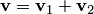де , где .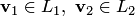

Действительно, если предположить противное, а именно существование двух разных разложений: 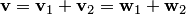, где 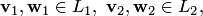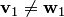, то получим противоречие: из равенства 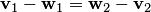следует, что ненулевой вектор 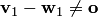принадлежит обоим подпространствам 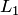и 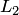одновременно, значит, принадлежит их пересечению, а по определению их пересечение состоит из одного нулевого вектора.