Вычисление поверхностного интеграла 1 рода 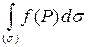 сводится к вычислению двойного интеграла. Рассмотрим несколько случаев.
сводится к вычислению двойного интеграла. Рассмотрим несколько случаев.
Случай 1. Пусть гладкая поверхность  задана параметрическими уравнениями
задана параметрическими уравнениями
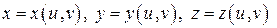 или
или 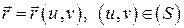 .
.
По определению, поверхностный интеграл функции  по поверхности
по поверхности 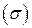 есть предел интегральной суммы функции
есть предел интегральной суммы функции  , который не зависит от способа разбиения поверхности
, который не зависит от способа разбиения поверхности 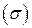 на ячейки:
на ячейки:
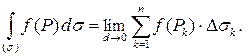
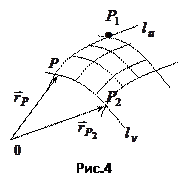 Удобно разбить поверхность
Удобно разбить поверхность 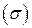 на ячейкикоординатными линиями
на ячейкикоординатными линиями 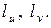 Выделим одну из таких ячеек (рис. 4). Рассмотрим радиус-векторы точек
Выделим одну из таких ячеек (рис. 4). Рассмотрим радиус-векторы точек 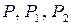 :
: 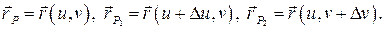 Тогда
Тогда 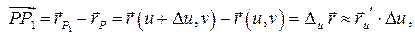
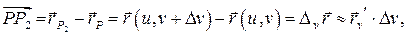
и площадь ячейки 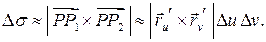
По аналогии с этим элемент площади поверхности
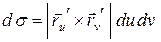 .
.
Можно показать (строгое доказательство опускаем), что
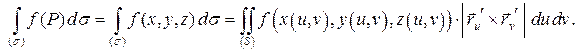
Итак, получили следующее правило:
Для вычисления поверхностного интеграла 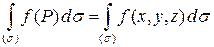 следует
следует
1) в подынтегральной функции подставить вместо 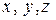 их значения на поверхности
их значения на поверхности  , т.е.
, т.е. 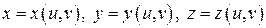 ,
,
2) заменить элемент площади 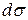 на выражение
на выражение 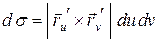 ;
;
3) вычислить получившийся двойной интеграл по области 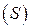 изменения переменных
изменения переменных 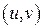 .
.
Случай 2. Пусть гладкая поверхность  задана уравнением, разрешенным относительно
задана уравнением, разрешенным относительно 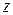 :
: 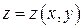 . Присоединив два очевидных тождества, получим параметрические уравнения поверхности
. Присоединив два очевидных тождества, получим параметрические уравнения поверхности 
 (
(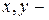 параметры); тогда
параметры); тогда 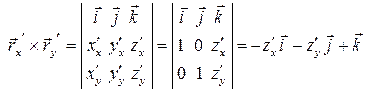 ,
,
и по формуле (7.34) получим 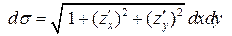 .
.
Итак, для вычисления поверхностного интеграла 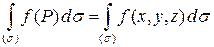 следует:
следует:
1) в подынтегральной функции заменить 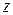 его значением
его значением 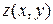 на поверхности
на поверхности  ,
,
2) заменить элемент площади 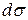 на выражение
на выражение 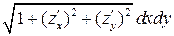 ,
,
3) вычислить получившийся двойной интеграл по проекции 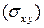 поверхности
поверхности  на плоскость
на плоскость 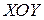 .
.
Случай 3. Пусть гладкая поверхность  задана уравнением, разрешенным относительно
задана уравнением, разрешенным относительно  :
: 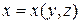 . Тогда
. Тогда
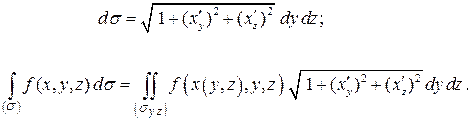
Здесь 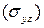 есть проекция поверхности
есть проекция поверхности  на плоскость
на плоскость 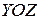 .
.
Случай 4. Пусть гладкая поверхность  задана уравнением, разрешенным относительно
задана уравнением, разрешенным относительно 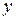 :
: 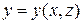 . Тогда
. Тогда
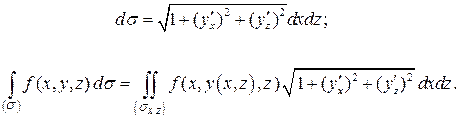
Здесь 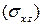 есть проекция поверхности
есть проекция поверхности  на плоскость
на плоскость 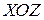 .
.
Пример 1. Найти массу однородной поверхности 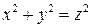 ,
, 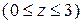 , если
, если 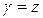 .
.

|
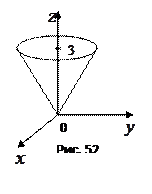 Решение. Построим поверхность
Решение. Построим поверхность 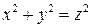 методом сечений. В сечении
методом сечений. В сечении 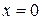 получаем
получаем 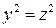 или
или 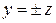 . Это – пара прямых в плоскости
. Это – пара прямых в плоскости 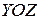 (рис. 5). В сечении
(рис. 5). В сечении 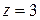 получаем окружность
получаем окружность 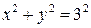 . Таким образом, уравнение
. Таким образом, уравнение 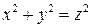 определяет коническую поверхность. Массу поверхности найдем с помощью поверхностного интеграла:
определяет коническую поверхность. Массу поверхности найдем с помощью поверхностного интеграла: 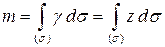 .
. Для вычисления этого интеграла уравнение поверхности удобно разрешить относительно 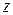 :
: 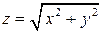 . Найдем
. Найдем 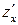 ,
, 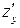 и затем
и затем 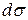 по первой из формул:
по первой из формул: 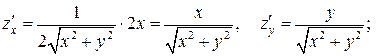
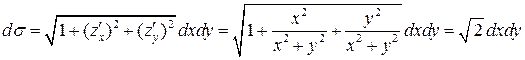 .
.
Теперь вычислим 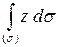 , подставляя значение
, подставляя значение 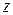 на поверхности
на поверхности 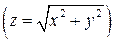 и
и
значение 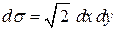 :
:
 .
.
Здесь 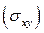 есть проекция конической поверхности
есть проекция конической поверхности  на плоскость
на плоскость 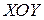 , т.е. круг радиусом
, т.е. круг радиусом 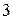 (рис. 5). Двойной интеграл по кругу удобнее вычислять в полярной системе координат. Для этого заменим
(рис. 5). Двойной интеграл по кругу удобнее вычислять в полярной системе координат. Для этого заменим 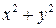 на
на 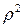 , а
, а 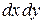 на
на 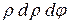 . Получим
. Получим
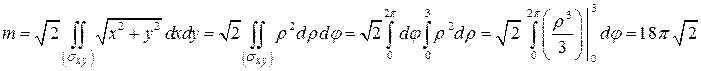 .
.
Пример 2. Найти момент инерции относительно начала координат полусферы 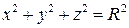 ,
, 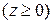 , если плотность
, если плотность 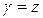 .
.
Решение. Момент инерции относительно начала координат поверхности найдем с помощью поверхностного интеграла по второй из формул (6.13):
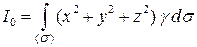 .
.
На поверхности сферы 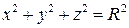 ,
, 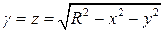 . Поэтому
. Поэтому
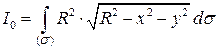 .
.
Для вычисления этого интеграла разрешим уравнение поверхности относительно 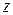 , найдем
, найдем 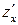 ,
, 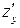 и затем
и затем 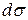 по первой из формул:
по первой из формул:
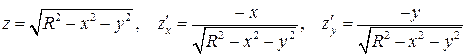 ;
;
 .
.
Подставляя выражение для 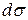 в интеграл, получим
в интеграл, получим
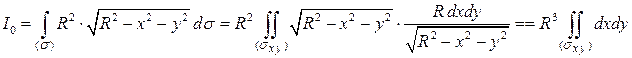 .
.
Проекция 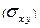 полусферы на плоскость
полусферы на плоскость 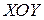 есть круг радиусом
есть круг радиусом 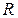 ;
;  равен площади
равен площади 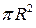 этого круга. Поэтому
этого круга. Поэтому 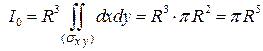 .
.
12. Лекционное занятие. ТЕОРИЯ СКАЛЯРНОГО И ВЕКТОРНОГО ПОЛЯ
 2014-02-02
2014-02-02 1441
1441
