Задачи, приводящие к уравнениям эллиптического типа

Лекция 18. СТАЦИОНАРНЫЕ УРАВНЕНИЯ. УРАВНЕНИЕ ЛАПЛАСА И МЕТОДЫ ЕГО РЕШЕНИЯ

Рассмотрим движение несжимаемой жидкости. Пусть некий произвольный фиксированный объем V жидкости, ограниченный поверхностью S, и массой т движется со скоростью 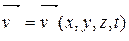. Масса т связана с плотностью 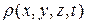соотношением

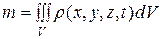. (18.1)

Эта масса может изменяться за счет потока жидкости через поверхность S, причем

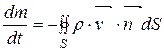, (18.2)

где 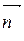- внешняя нормаль к S. Тогда из уравнений (18.1) и (18.2) получаем

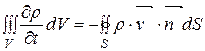. (18.3)

Преобразуя поверхностный интеграл, находящийся в правой части выражения (18.3) по формуле Остроградского (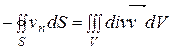), запишем формулу (18.3) в виде

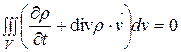Отсюда в силу произвольности выделенного объема V следует

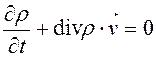Это уравнение называют уравнением неразрывности сплошной среды. Для несжимаемой жидкости плотность 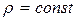, и из уравнения неразрывности следует, что

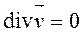. (18.4)

Рассмотрим установившееся течение несжимаемой жидкости, для которого 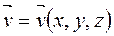. Если это течение безвихревое, то существует потенциал скоростей , такой, что

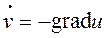. (18.5)

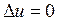или

, или 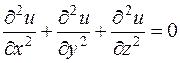, (18.6)

т.е. потенциал скоростей удовлетворяет уравнению (18.6), которое является уравнением эллиптического типа и называется уравнением Лапласа.

Запишем теорему Гаусса для электростатического поля напряженностью 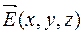в вакууме

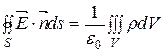. (18.7)

где 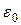- электрическая постоянная в системе Си; 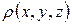- объемная плотность электрических зарядов; V – некоторый объем пространства, ограниченный замкнутой поверхностью S. С помощью теоремы Остроградского соотношение (18.7) можно преобразовать к дифференциальной форме

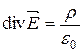. (18.8)

Поскольку напряженность поля связана с потенциалом этого поля соотношением

,

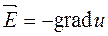то из (18.8) получим уравнение для потенциала электростатического поля

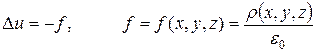, (18.9)

которое будет являться уравнением эллиптического типа и называться уравнением Пуассона.

Как и уравнение Лапласа, так и уравнение Пуассона являются стационарными уравнениями, т.к. искомая функция не зависит от времени.

Уравнение Лапласа можно записать не только в системе декартовых координат (18.6), но и цилиндрической системе

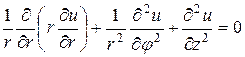(18.10)

и сферической системе координат

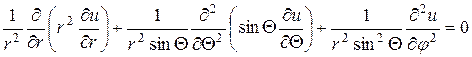. (18.11)

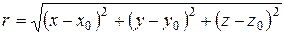С уравнением Лапласа связано понятие гармонической функции. Функцию называют гармонической в некоторой области D, если в этой области она непрерывна вместе со своими частными производными до второго порядка включительно и удовлетворяет уравнению Лапласа. Так, если функция зависит только от расстояния точки 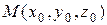до начала координат, то уравнение Лапласа будет иметь вид

,

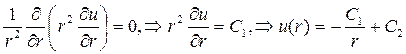если С ₁ = -1, а С ₂ = 0, то функция 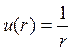будет гармонической функцией везде в области D за исключением точки 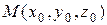и будет называться фундаментальным решением уравнения Лапласа в пространстве.

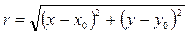Если функция зависит только от расстояния точки 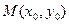до начала координат, то уравнение Лапласа будет иметь вид

,

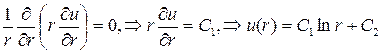и если С ₁ = -1, а С ₂ = 0, то функция 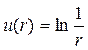будет гармонической функцией везде в области D за исключением точки и будет называться фундаментальным решением уравнения Лапласа на плоскости.