Теорема 1.5. Предел суммы конечного числа функций равен сумме пределов этих функций, т. е.
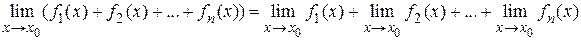 .
.
Д о к а з а т е л ь с т в о. Используем теорему 1.3.
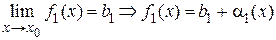 ,
,
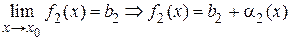 ,
,
………………………………………..
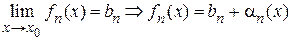 ,
,
где 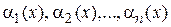 - бесконечно малые функции при
- бесконечно малые функции при 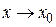 .
.
Сумму левых частей равенств приравняем сумме правых частей, получим
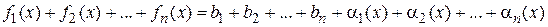 . Так как сумма
. Так как сумма 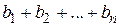 является постоянной, а сумма конечного числа бесконечно малых функций
является постоянной, а сумма конечного числа бесконечно малых функций 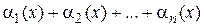 - бесконечно малой функцией по первому свойству бесконечно малых функций, то по теореме 1.4
- бесконечно малой функцией по первому свойству бесконечно малых функций, то по теореме 1.4 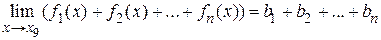
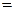
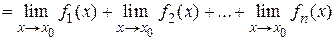 .
.
Теорема 1.6. Предел произведения функций равен произведению пределов этих функций, т. е. 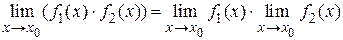 .
.
Д о к а з а т е л ь с т в о. Пусть существуют пределы 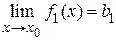 и
и
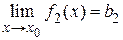 . По теореме 1.3
. По теореме 1.3 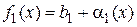 ,
, 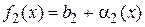 , где
, где 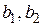 - постоянные величины,
- постоянные величины, 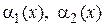 - бесконечно малые функции при
- бесконечно малые функции при 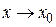 . Тогда
. Тогда 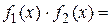
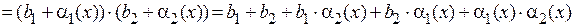 .
.
Так как сумма 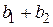 является постоянной величиной, а
является постоянной величиной, а 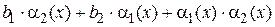 является бесконечно малой функцией по свойствам 1 и 2 бесконечно малых функций, то по теореме 1.4
является бесконечно малой функцией по свойствам 1 и 2 бесконечно малых функций, то по теореме 1.4
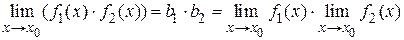 .
.
Следствие 1. Постоянную величину можно выносить за знак предела, т.е.
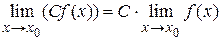 .
.
Следствие 2. Предел степени функции равен степени предела функции, т. е. 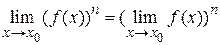 .
.
Теорема 1.7. Предел частного функций равен частному пределов функций, если предел функции, стоящей в знаменателе, отличен от нуля, т. е.
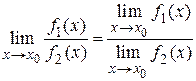 .
.
Д о к а з а т е л ь с т в о. Пусть 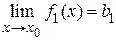 ,
, 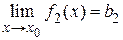 ,
, 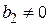 .
.
На основании теоремы 1.3 имеем 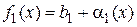 ,
, 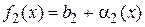 .
.
Найдем разность функции 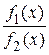 и постоянной
и постоянной 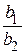 .
.
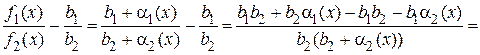
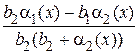 .
.
Согласно свойствам бесконечно малых функций данная разность является бесконечно малой функцией, следовательно, по теореме 1.4 предел функции 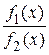 равняется постоянной
равняется постоянной 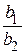 , т. е.
, т. е. 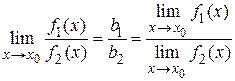 .
.
 2015-02-27
2015-02-27 2172
2172








