Определение бесконечно малой функции. Функция a(x) называется бесконечно малой функцией при 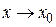 , если для любого сколь угодно малого положительного числа e существует такое положительное число d, зависящее от e, что для любого x, принадлежащего d-окрестности
, если для любого сколь угодно малого положительного числа e существует такое положительное число d, зависящее от e, что для любого x, принадлежащего d-окрестности 
 a(x) находится в e-окрестности начала координат a(x)Î
a(x) находится в e-окрестности начала координат a(x)Î 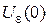 , т.е.
, т.е. 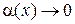 .
.
В краткой записи на языке «e-d» данное определение имеет вид
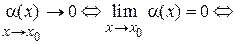
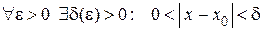
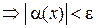 .
.
Ни какое малое число (например, 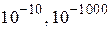 и т. д.) не является бесконечно малой величиной, кроме числа
и т. д.) не является бесконечно малой величиной, кроме числа 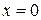 .
.
Определение бесконечно большой функции. Функция 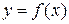 называется бесконечно большой при
называется бесконечно большой при 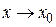 , если для любого сколь угодно большого положительного числа N существует такое положительное число
, если для любого сколь угодно большого положительного числа N существует такое положительное число 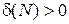 , зависящее от N, что если x принадлежит d-окрестности числа
, зависящее от N, что если x принадлежит d-окрестности числа  (
(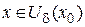 ), то абсолютная величина значения функции больше числа N (
), то абсолютная величина значения функции больше числа N (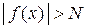 ), т.е.
), т.е. 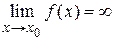 .
.
Иначе, можно кратко записать
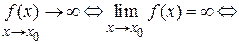
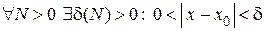
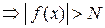 .
.
Теорема 1.2. Функция, обратная по величине к бесконечно малой функции является бесконечно большой и, наоборот, функция, обратная по величине к бесконечно большой, является бесконечно малой функцией.
Д о к а з а т е л ь с т в о.
1. Пусть a(x) бесконечно малая функция, т. е. 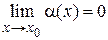 . Докажем, что
. Докажем, что 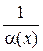 является бесконечно большой, т. е.
является бесконечно большой, т. е. 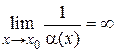 . Пусть N произвольно выбранное сколь угодно большое положительное число. Так как
. Пусть N произвольно выбранное сколь угодно большое положительное число. Так как 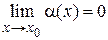 , то для любого e, в том числе и для
, то для любого e, в том числе и для 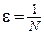 >0, существует такая d-окрестность
>0, существует такая d-окрестность  , что "
, что " 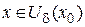
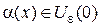 , т. е.
, т. е. 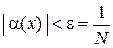 . Однако,
. Однако, 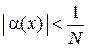 равносильно
равносильно 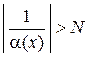 . Следовательно, для значений х, принадлежащих таким образом выбранной окрестности
. Следовательно, для значений х, принадлежащих таким образом выбранной окрестности  , функция
, функция 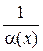 по абсолютной величине больше произвольно выбранного сколь угодно большого числа N, а это означает, что
по абсолютной величине больше произвольно выбранного сколь угодно большого числа N, а это означает, что 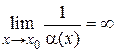 .
.
2. Пусть 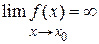 . Докажем, что
. Докажем, что 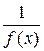 является бесконечно малой функцией, т.е.
является бесконечно малой функцией, т.е. 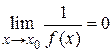 . Так как
. Так как 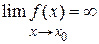 , то для любого N, в том числе и для
, то для любого N, в том числе и для 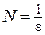 >0, где e произвольно выбранное сколь угодно малое положительное число, существует такая d-окрестность
>0, где e произвольно выбранное сколь угодно малое положительное число, существует такая d-окрестность  , что "
, что " 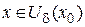
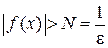 . Однако,
. Однако, 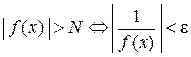 . Следовательно, для значений х, принадлежащих таким образом выбранной окрестности
. Следовательно, для значений х, принадлежащих таким образом выбранной окрестности  , функция
, функция 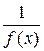 по абсолютной величине меньше произвольно выбранного числа e, а это означает, что
по абсолютной величине меньше произвольно выбранного числа e, а это означает, что 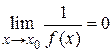 .
.
Например, если 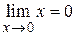 , то
, то 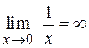 , и наоборот, если
, и наоборот, если 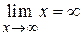 , то
, то 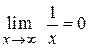 .
.
Данная теорема часто используется при нахождении пределов дробно-рациональных функций.
 2015-02-27
2015-02-27 3063
3063
