Теорема 1.3. Если функция имеет предел 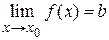 , то ее можно представить в виде суммы предела и бесконечно малой функции, т.е.
, то ее можно представить в виде суммы предела и бесконечно малой функции, т.е. 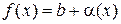 , где
, где 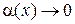 при
при 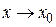 .
.
Д о к а з а т е л ь с т в о. По определению предела 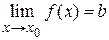
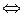
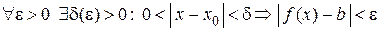 . Отсюда следует, что
. Отсюда следует, что 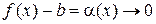 при
при 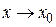 , т. е.
, т. е. 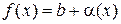 .
.
Теорема 1.4. Если функция 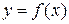 равняется сумме постоянной b и бесконечно малой функции
равняется сумме постоянной b и бесконечно малой функции 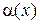 , т. е.
, т. е. 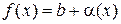 , где
, где 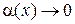 при
при 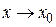 , то эта постоянная является ее пределом, т. е.
, то эта постоянная является ее пределом, т. е. 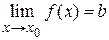 .
.
Д о к а з а т е л ь с т в о. Пусть 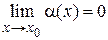 ,
, 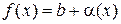 .
.
Отсюда следует 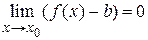 . В самом деле
. В самом деле 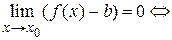
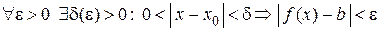 , т. е.
, т. е. 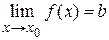 .
.
 2015-02-27
2015-02-27 1135
1135








