Первый замечательный предел. Теорема 1.8 о промежуточной функции

Теорема 1.8 о промежуточной функции.

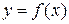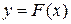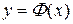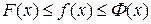
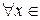
Если в некоторой d-окрестности точки значения функции заключены между значениями функций и , т. е. и при этом 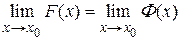= b, то .

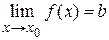Д о к а з а т е л ь с т в о. Пусть .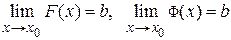

Тогда ,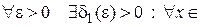

.

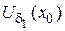
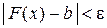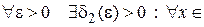
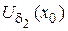
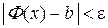Выберем 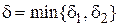, тогда

.

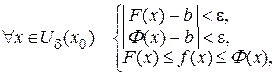
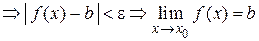Теорема 1.9 о первом замечательном пределе.

Для любой бесконечно малой функции 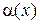предел отношения 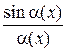равен единице, т. е. . (1.1)

Д о к а з а т е л ь с т в о. Рассмотрим окружность радиуса R с центром вточке О, сектор OAB с углом a и треугольники OAB, OAС, (АС – касательная к окружности) (рис. 8).

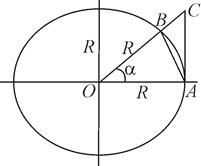
Рис. 8

Очевидно, для площадей этих фигур справедливо соотношение

.

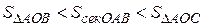Площади треугольников и сектора найдем по известным формулам, получим

.

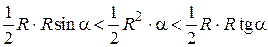Умножим данное неравенство на 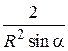, имеем .

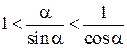Для обратных величин этого неравенства справедливо соотношение

.

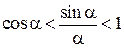Так как 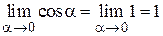, то по теореме о промежуточной функции

.

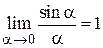Бесконечно малые функции, предел отношения которых равен единице, называются эквивалентными. Записывают 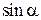~ a.

Пример 1.5. .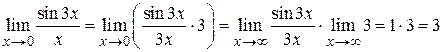

Пример 1.6. .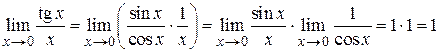

Это значит, что tg x и х являются эквивалентными функциями (tg x ~ х).