Пусть на отрезке [ a, b ] задана функция y = f (x). Точки х и  принадлежат интервалу (a, b). Разность
принадлежат интервалу (a, b). Разность 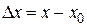 называется приращением независимой переменной х в точке
называется приращением независимой переменной х в точке  , а
, а 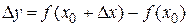 - приращением функции в точке
- приращением функции в точке  при данном приращении D х (рис. 9).
при данном приращении D х (рис. 9).
Пример 1.17. Найти приращения функций y = sin x и 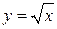 в точке
в точке  при приращении аргумента
при приращении аргумента 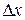 .
.
Находим: 1) 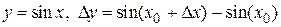 ;
;
2) 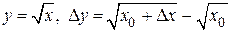 .
.
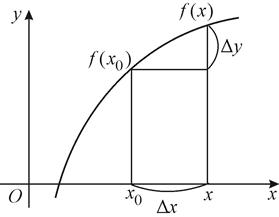
Рис. 9
Определение 1. Функция 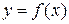 называется непрерывной в точке
называется непрерывной в точке  , если она определена в окрестности этой точки и бесконечно малому приращению независимой переменной
, если она определена в окрестности этой точки и бесконечно малому приращению независимой переменной 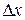 соответствует бесконечно малое приращение функции D y, т. е.
соответствует бесконечно малое приращение функции D y, т. е.
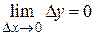 . (1.4)
. (1.4)
Например, функция y = С является непрерывной в любой точке х Î(-¥; +¥), так как 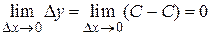 .
.
Функция y = х так же является непрерывной в любой точке х Î(-¥; +¥), так как 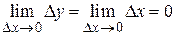 .
.
Преобразуем условие непрерывности (1.4)
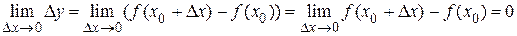 .
.
Так как 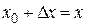 ,
, 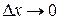 , то
, то 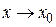 . Учитывая это, получим
. Учитывая это, получим
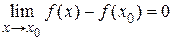 или
или 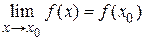 .
.
Последнее равенство можно записать следующим образом:
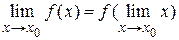 .
.
Таким образом, если функция непрерывная, то предел от функции равен функции от предела независимой переменной, т. е. можно переходить к пределу под знаком непрерывной функции.
Определение 2. Функция 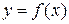 называется непрерывной в точке
называется непрерывной в точке  , если она определена в окрестности этой точки и предел функции в этой точке равен значению функции в предельной точке, т. е.
, если она определена в окрестности этой точки и предел функции в этой точке равен значению функции в предельной точке, т. е.
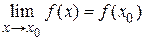 . (1.5)
. (1.5)
Определение 3. Функция 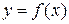 называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой внутренней точке этого отрезка и односторонние пределы функции в граничных точках равны значениям функции в этих точках, т. е.
называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой внутренней точке этого отрезка и односторонние пределы функции в граничных точках равны значениям функции в этих точках, т. е. 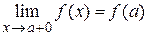 ,
, 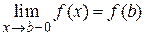 .
.
 2015-02-27
2015-02-27 524
524








