Действия над непрерывными функциями

Теорема 1.11. Если функци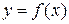и и 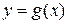непрерывны в точке , то в этой точке также непрерывны следующие функции:

1) ;

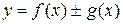2) ;

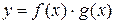3) 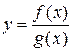, где .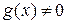

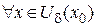Д о к о з а т е л ь с т в о. Используем второе определение непрерывности функции в точке и свойства пределов, получим:

1) ;

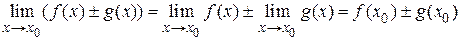2) ;

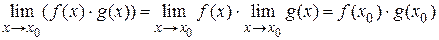3) .

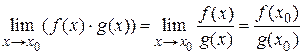Так как пределы от рассмотренных функций равняются значениям этих функций в предельной точке, то эти функции непрерывны.