1. Сравнить бесконечно малые функции 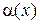 и
и 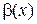 значит найти предел их отношения
значит найти предел их отношения 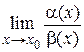 .
.
2. Бесконечно малые функции называются несравнимыми, если предел их отношения не существует.
Пример 1.11. Сравнить бесконечно малые функции
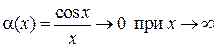 и
и 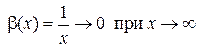 .
.
Находим, 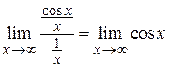 не существует. Следовательно, бесконечно малые функции
не существует. Следовательно, бесконечно малые функции 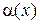 и
и 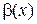 несравнимые.
несравнимые.
3. Бесконечно малые функции называются одного порядка малости, если предел их отношения равен отличной от нуля конечной величине.
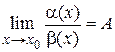 , где
, где 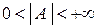 .
.
Пример 1.12. Сравнить бесконечно малые функции
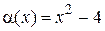 и
и 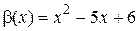 при х ® 2.
при х ® 2.
Находим 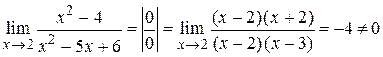 .
.
Следовательно, бесконечно малые функции 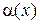 и
и 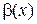 одного порядка малости.
одного порядка малости.
4. Бесконечно малые функции называются эквивалентными, если предел их отношения равен единице.

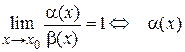 ~
~ 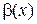 .
.
5. Бесконечно малая функция 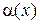 называется более высокого порядка малости по сравнению с бесконечно малой
называется более высокого порядка малости по сравнению с бесконечно малой 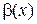 , если предел их отношения равен нулю
, если предел их отношения равен нулю
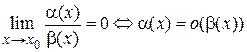 .
.
Запись 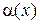 = о (
= о (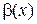 ) означает, что
) означает, что 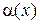 более высокого порядка малости по сравнению с
более высокого порядка малости по сравнению с 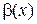 . (Здесь в записи используется о – буква «о» маленькая).
. (Здесь в записи используется о – буква «о» маленькая).
Пример 1.13. 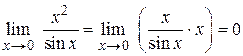 ,
, 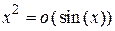 .
.
6. Бесконечно малая функция 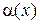 называется n -го порядка малости по сравнению с
называется n -го порядка малости по сравнению с 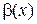 , если
, если 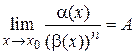 , где
, где 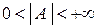 .
.
Пример 1.14. Определить порядок малости 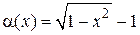 по сравнению с x при
по сравнению с x при 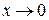 .
.
Находим
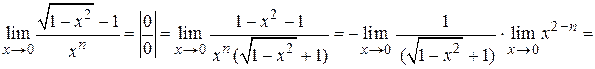
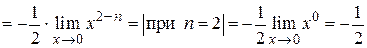 .
.
Следовательно, бесконечно малая функция 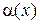 2-го порядка малости по сравнению с x.
2-го порядка малости по сравнению с x.
Теорема 1.10. Предел отношения бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями, т. е.
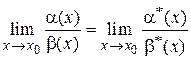 , где
, где 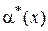 ~
~ 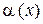 ,
, 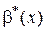 ~
~ 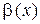 .
.
Д о к а з а т е л ь с т в о. Так как 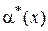 ~
~ 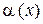 ,
, 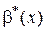 ~
~ 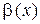 , получаем
, получаем
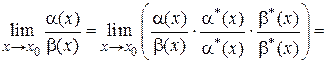
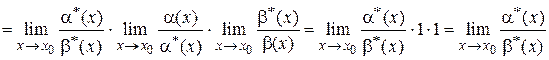 .
.
Пример 1.16. Найти предел  .
.
Так как sin3 x ~ 3 x и tg5 x ~ 5 x, то 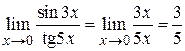 .
.
 2015-02-27
2015-02-27 2478
2478
