2015-02-27
1754
Положительным направлением крутящего момента, расположенного в сечении, считается направление момента против часовой стрелки.
Для нахождения касательного напряжения τρ в любой точке поперечного сечения вала, находящийся на расстоянии ρ от центра (см. рис. 8) справедлива следующая формула:
τρ =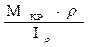 
(29)
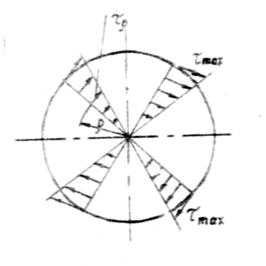
Рис.10
Условие жесткости при кручении имеет вид: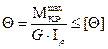 
, где [ 
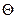] –допускаемый угол имеет размерность рад/м в данной формуле.
При расчетах на жесткость находят максимальный относительный угол закручивания: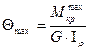 
(30)
и сравнивают его с допускаемым [ ]: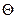
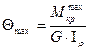
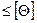(31)
Чтобы перейти к 
размерности град/м условие жесткости должно иметь следующий вид:
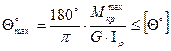, (32)
где [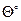 
] - относительный угол закручивания имеет размерность град/м, величина лежит в пределах от 0,25 град/м до 1 град/м и зависит от назначения вала.
Величина-G Iρ (произведение модуля упругости второго рода G на полярный момент инерции площади поперечного сечения Iρ)- называется жесткостью сечения вала при кручении и показывает влияние материала и геометрического размера сечения вала на получаемую деформацию.
Угол закручивания круглого стержня в пределах упругих деформаций рассчитывают по следующей формуле:
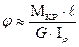(33)
где Мкр - крутящий момент,
ℓ - длина вала,
G - модуль сдвига
Iρ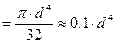 
- полярный момент инерции площади поперечного сечения сплошного стержня диаметром d,
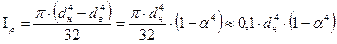- полярный момент инерции трубчатого стержня с внутренним диаметром 
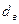и наружным диаметром 
, 
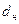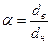
G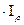 
- жесткость сечения стержня при кручении, кГ 
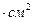(МПа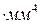 
).
Чтобы получить формулу (29) для определения касательного напряжения τ в любой точке сечения стержня и формулу (30)для определения относительного угла закручивания круглого стержня , необходимо рассмотреть некоторый участок вала длиной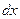 
(см. рис. 9).
Рис. 11
Вал подвержен действию некоторого скручивающего момента Мк, вызывающего внутренний крутящий момент Мкр
Пусть угол поворота одного из сечений m-m выделенного элемента вала будет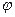 
, тогда угол поворота другого сечения n-n элементарного участка 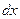будет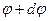 
, т. е. угол закручивания участка стержня длиной 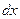будет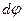 
. Следовательно, если до деформации радиус 
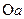сечения m-m и радиус 
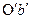сечения n-n находились в одной диаметральной плоскости, то после деформации кручения радиус 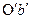займёт положение 
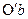, составляющее угол 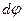с его положением 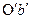до деформации. Образующая 
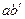после деформации займёт некоторое новое положение 
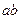под углом 
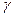к её первоначальному положению .
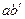Угол 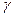между образующим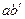и и 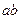представляет cобой не что иное как относительный сдвиг, или угол сдвига:
tg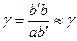 
.
Учитывая, что 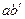= 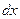, а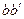 
= 
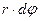, угол сдвига можно представить в виде
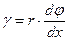(34)
Величина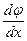 
, как уже известно (см. пункт 3 основных гипотез, принятых при кручении), является относительным (погонным) углом закручивания и обозначается через 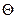. Учитывая это формулу (33)можно записать так:
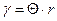. (35)
Теперь рассмотрим физическую сторону задачи, устанавливающую связь между напряжением и деформацией. Поскольку элемент испытывает чистый сдвиг, то, учитывая выражение (10) согласно формуле (1) получим:
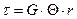. (36)
Так как при закручивании поперечные сечения вала остаются плоскими, а радиусы прямыми (см. пункт 1 гипотез, принятых при кручении), то выражения для угла сдвига и касательного напряжения в сечении на расстоянии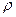 
от центра его можно представить формулами, аналогичными формулам (35)и (36):
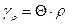; (37)
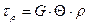. (38)
Формула (37) показывает, что касательные напряжения в поперечном сечении изменяются по линейному закону прямо пропорционально расстоянию 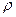точек от центра сечения (см. рис. 10). Очевидно, максимальные напряжения будут у поверхности стержня, при 
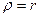. Таким образом, выражение (38)можно переписать в виде:
.
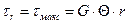Так как Мкр будет единственным усилием в сечении вала, представляющим собой суммарный момент от касательных напряжений, действующих в плоскости поперечного сечения:
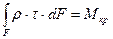(39)
Подставляя выражение (38) для касательного напряжения в уравнение (39), будем иметь:
.
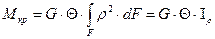Отсюда получим формулу для определения относительного угла закручивания круглого стержня (см. формулу (30)), указанную ранее:
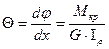(40 )
Зная выражение ( 24)относительного угла закручивания, можно записать формулу для определения взаимного угла закручивания двух сечений, расположенных на расстоянии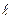 
:
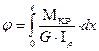. (41)
Если в пределах цилиндрического участка стержня длиною 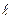крутящие моменты в сечениях не изменяются, то
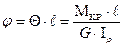(42)
Формулу ( 42 ), устанавливающую связь между силовым фактором при кручении (Мкр) и соответствующей деформацией кручения (углом 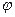), часто называют законом Гука при кручении.
Для определения касательного напряжения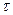 
в любой точке сечения стержня достаточно в формулу (38)подставить выражение для по формуле (40). Тогда:
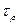
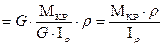(43)
Формула (43) аналогична формуле (29), что и требовалось доказать.
Если в стержне выделить прямоугольный элемент, грани которого повернуты относительно исходных плоскостей на угол α и воспользоваться формулами, связывающими нормальные напряжения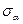 
и касательные напряжения 
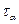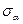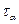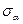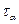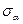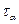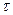приложенные к исходным площадкам под углом α: =τ∙sin2α и =τ∙cos2α. При α=00 и α=900 напряжения и принимают значения, соответствующие исходным площадкам, т. е. =0, а = . При α=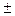 
450 касательные напряжения 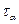=0, а нормальные напряжения = .
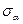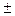
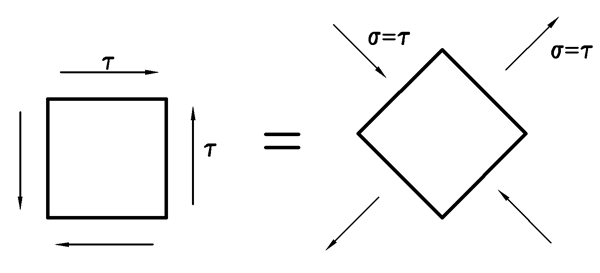
Рис. 12
Касательные напряжения в любой точке поперечного сечения при упругом кручении можно определить по формуле:
τρ = ,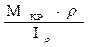
где ρ - расстояние от центра сечения до точки, в которой определяется касательное напряжение.
Формула показывает, что напряжения в плоскости сечения вала распределены неравномерно и в зависимости от радиуса изменяются по линейному закону от нуля в центре сечения, до максимума на его поверхности (см. рис. 10).
Известно, что касательные напряжения в наклонных площадках определяются по формуле: 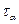=τ∙cos2α. Вычислим значение касательного напряжения на площадке, расположенной под углом 900 к наклонной.
Тогда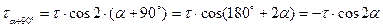 
.
Значит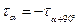 
.
Касательные напряжения на взаимно перпендикулярных площадках равны по величине и направлены навстречу друг другу.
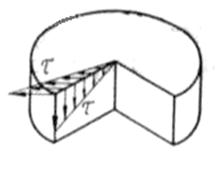
Рис. 13
В силу закона парности действия касательных напряжений в осевых (продольных) сечениях также возникнут касательные напряжения. Таким образом, при кручении касательные напряжения действуют в поперечных и продольных сечениях вала, направленные от ребра или к ребру (см. рис. 12, 13).
При кручении материал вала находится в состоянии чистого сдвига, поэтому в сечениях, наклоненных под углом 450 к граням, на которых действуют касательные напряжения, будут действовать только нормальные напряжения, численно равные касательным. Таким образом, чистый сдвиг
может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям (см. рис. 12 и рис. 14).
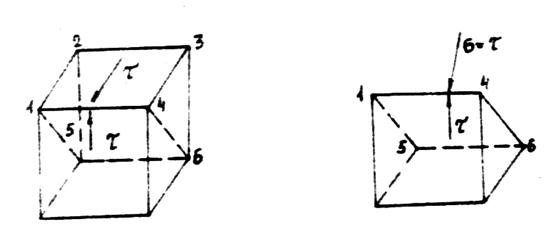
Рис. 14
Характер разрушения вала будет зависеть от способности материала сопротивляться касательным и нормальным напряжениям.
Если материал сопротивляется сдвигу хуже, чем растяжению (сталь), то образец разрушается по сечению, нормальному к его оси (см. рис. 15).
Если на образце начертить продольную, прямую линию, то после разрушения линия будет винтовой. Количество витков будет равно количеству полных углов закручивания. Полный угол закручивания равен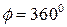 
.
Если же материал сопротивляется растяжению хуже, чем сдвигу (чугун), то трещины при кручении пойдут по винтовым линиям, касательные к которым образуют угол 450 с осью стержня (см. рис 16).
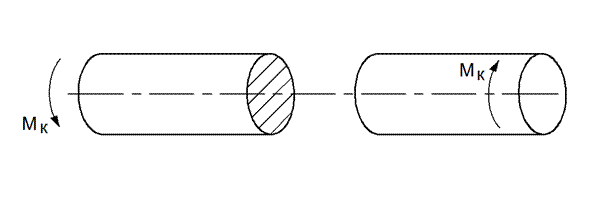
Рис. 15. Вид разрушения образца из стали.
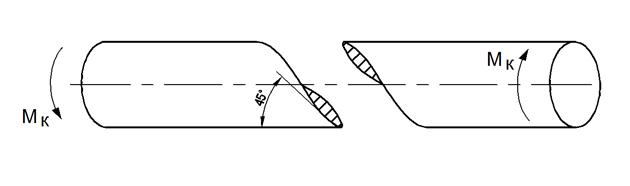
Рис. 16. Вид разрушения образца из чугуна.
