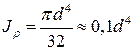Момент инерции относительно оси, параллельной центральной (теорема Штейнера)

Теорема Штейнера:

Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.

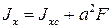(15)

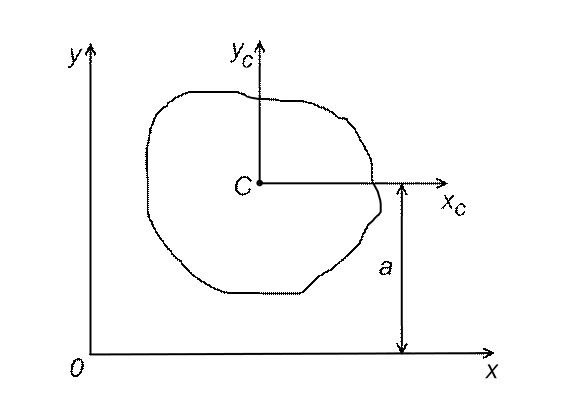
Рис. 4

Доказательство теоремы Штейнера.

Согласно рис. 5 расстояние у до элементарной площадки dF

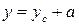
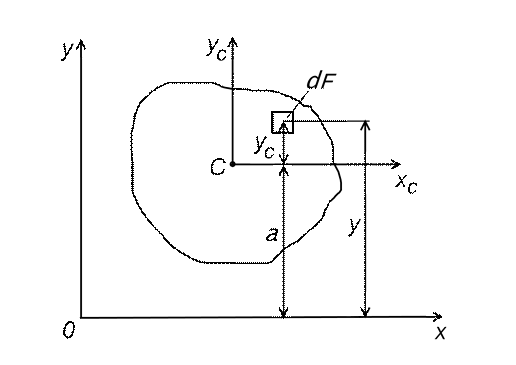
Рис. 5

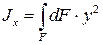
Подставляя значение у в формулу, получим:

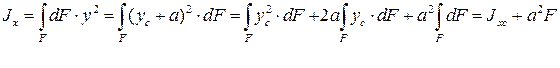
Слагаемое 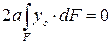, так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).

Для прямоугольника высотой h и шириной b:

Осевой момент инерции:

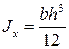
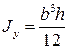
Момент сопротивления изгибу:

момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:

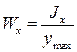
т.к. 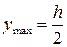, то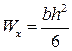

Для круга:

Полярный момент инерции:

Осевой момент инерции: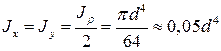

Момент сопротивления кручению: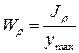

Т.к. 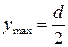, то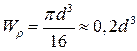

Момент сопротивления изгибу: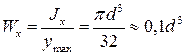

Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.

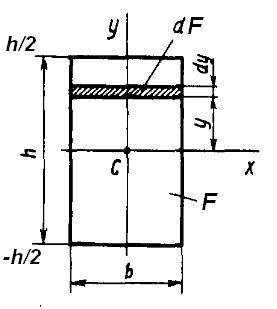
Рис. 6

Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b (ширина) и dy (высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF = bdy. Вычислим значение осевого момента инерции J_x

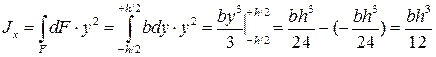
По аналогии запишем

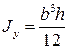- осевой момент инерции сечения относительно центральной

оси у

Центробежный момент инерции

, так как оси Сx и С y являются осями симметрии.

Пример 3. Определить полярный момент инерции круглого сечения.

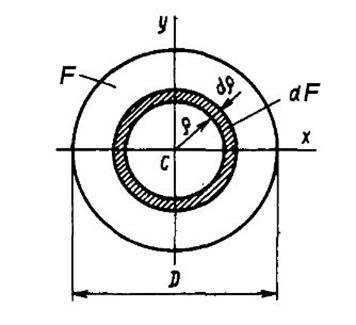
Рис. 7

Решение. Разобьём круг на бесконечно тонкие кольца толщиной 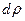радиусом 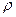, площадь такого кольца 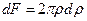. Подставляя значение 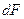в выражение для полярного момента инерции интегрируя, получим

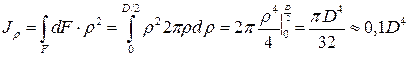
Учитывая равенство осевых моментов круглого сечения 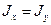и

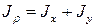, получаем

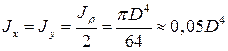
Осевые моменты инерции для кольца равны

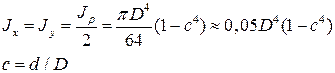
с – отношение диаметра выреза к наружному диаметру вала.