2015-02-27
3603
Условия параллельности и перпендикулярности прямых, если прямые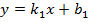 
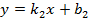параллельны, та угол 
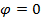и 
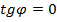, откуда из формулы (9) 
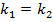. И наоборот, если 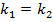, то по формуле (9) 
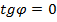и.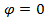 
Таким образом, равенство угловых коэффициентов является необходимым и достаточным условием параллельности двух прямых.
Если прямые перпендикулярны, то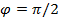 
, при этом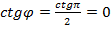 
или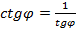 
= 
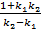, откуда 
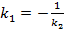или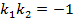 
.
Справедливо также и обратное утверждение. Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
Если прямые заданы общими уравнениями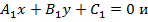 
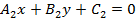, то учитывая, что их угловые коэффициенты 
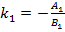и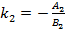 
, условие параллельности прямых 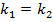примет вид 
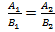. Следовательно, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных x и y.
Условие перпендикулярности прямых 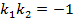в этом случае примет вид 
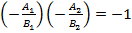, т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.
5. Расстояние от точки до данной прямой.
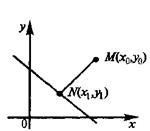
Рис.8
Пусть даны точка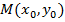 
и прямая 
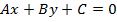. Под расстоянием от точки М до прямой АВ понимается длина перпендикуляра 
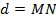, опущенного из точки М до прямой АВ.
Для определения расстояния d необходимо:
а) составить уравнение прямой MN, перпендикулярной данной и проходящей через точку ;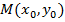
б) найти точку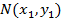 
пересечения прямых, решив систему уравнений этих прямых;
в) по формуле модуля вектора определить расстояние между двумя точками, т.е. найти
d = MN.
В результате преобразований получим
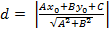. (10)
