2015-04-12
889
l 1: 
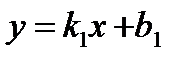, где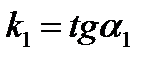 
l 2: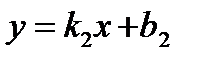 
, где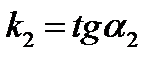 
Дано: l 1|| l 2.
Доказать: k 1= k 2.
1 способ: l 1|| l 2⇒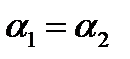 
⇒ 
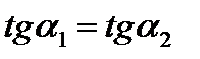, т.е. k 1= k 2
2 способ: l 1|| l 2⇒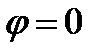 
⇒ 
⇒ 
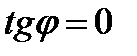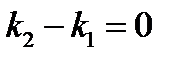,т.е. k 1= k 2
Обратно
Дано: k 1= k 2
Доказать: l 1|| l 2
k 1= k 2⇒ 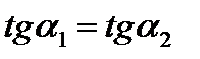⇒ ⇒ 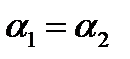l 1|| l 2
k 1= k 2 (7) – необходимое и достаточное условие параллельности двух прямых.
Условие перпендикулярности прямых
Дано: l 1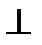 
l 2.
Доказать: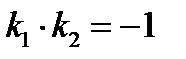 
(или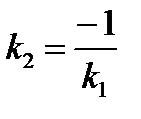 
).
Преобразуем (7):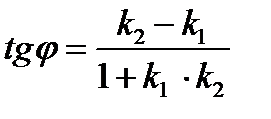 
, 
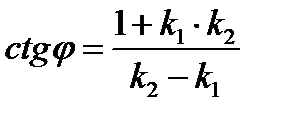
l 1 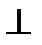l 2⇒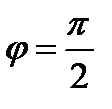 
⇒ 
⇒ 
⇒ 
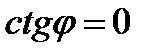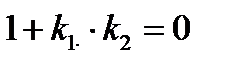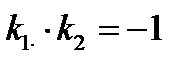
Справедливо и обратное: если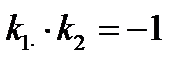 
, то l 1 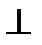l 2.
Итак,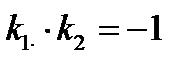 
– необходимое и достаточное
или 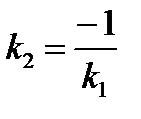условие перпендикулярности двух прямых.
