Трехуровневый симметричный периодический импульс

Часто в задачах проектирования приборов медицинского назначения требуется сформировать один или несколько сигналов гармонического вида (напри­мер, в электростимуляторах, реографах, синхронных детекторах, генераторах тональных сигналов в модемной связи и т.п.). Еще более сложной является задача создания нескольких сигналов, находящихся в определенных фазовых соотношениях.

При повышенных требованиях к стабильности частоты, фазы или амплитуды сигналов рационально синтезировать цифровыми методами гармонические или близкие к ним по частотному спектру сигналы. При этом применяют
различ­ные методы разложения (например, кусочно-постоянные функции Уолша).

Синтез колебаний выполняют с помощью цифровых схем или на основе микропроцессорных систем.

Простым, но в тоже время эффективным и наглядным примером является аппроксимация гармонического колебания трехуровневым периодическим импульсом. На Рис. 3.12 показан пример такого подхода для импульсов с единичными амплитудой и периодом (A =1; T =1).

Один период такого колебания можно представить в следующем виде (Рис. 3.12):

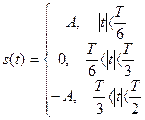
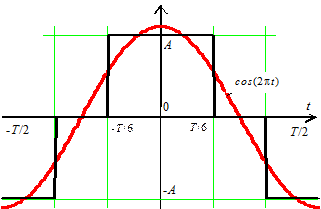
Рис. 3.12. Трехуровневый импульс

Коэффициенты ряда Фурье для положительных и целых n определяются следующим образом:

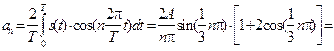
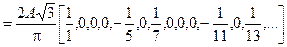
Здесь для упрощения в квадратных скобках приведены относительные амплитуды гармоник трехуровневого периодического колебания.

Все синусные коэффициенты b_n в данном случае равны нулю из-за четной симметрии сигнала. Тогда ряд Фурье имеет вид:

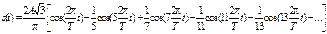
Спектр этого колебания (Рис. 3.13) не
содержит гармоник от основной до пятой, которая относительно основной уменьшена на 14 дБ.

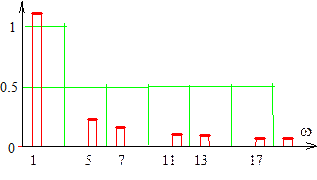
Рис. 3.13. Модуль спектра трехуровневого колебания (по оси абсцисс указаны номера гармоник)

Это существенно ослабляет требования к фильтру, выделяющему основную гармонику и подавляющему гармоники высших порядков, по сравнению с фильтрацией меандра т.к. в спектре трехуровневого колебания отсутствует 3-я гармоника и ряд более высокочастотных гармоник.