Последовательность униполярных прямоугольных импульсов

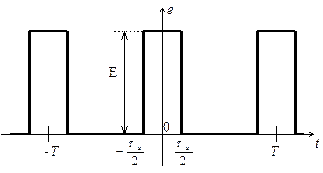
Рис. 3.10. Периодическая последовательность прямоугольных импульсов

Найдем постоянную составляющую как среднее значение сигнала за период:

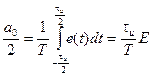
Коэффициент n -той гармоники:

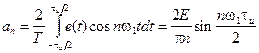(3.41)

Так как функция e (t) - четная, то b_n =0 и A_n = a_n:

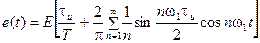(3.42)

Величину g =T/t_и называют скважностью импульсной последовательности. При больших значениях g спектр сигнала содержит очень большое число медле­н­но убывающих по амплитуде гармоник.

При этом расстояние между спектральными линиями очень мало, а амплитуды соседних гармоник близки по величине. Это следует из формулы (3.41), которую в данном случае удобно представить в измененном виде:

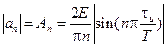
При малых значениях n можно считать что

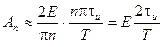
Постоянная составляющая, равная 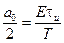, вдвое меньше амплитуды первой гармоники.

На Рис. 3.11 показан спектр импульсной последовательности при Т =1, t _и=0.05.

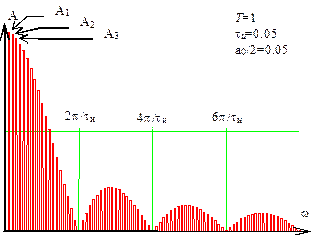
Рис. 3.11. Спектр последовательности