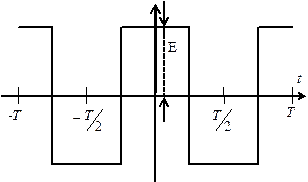
Рис. 3.1. Меандр с четной симметрией
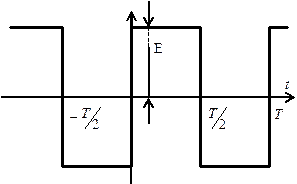
Рис. 3.2. Меандр с нечетной симметрией
Соответствующим выбором начала отсчета времени меандр можно представить в виде четной (Рис. 3.1) или нечетной (Рис. 3.2)функции.
Для нечетной функции применяя формулы (3.28) и (3.29) находим при s (t) =e (t):
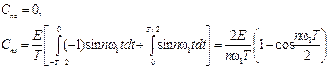 Учитывая, что T w1=2p, получаем:
Учитывая, что T w1=2p, получаем:
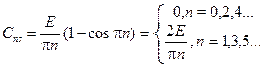
Начальные фазы y n в соответствии с (3.31), равны -p/2 для всех гармоник.
На Рис. 3.3показаны коэффициенты комплексного, а на Рис. 3.4тригонометрического ряда Фурье для меандра единичной амплитуды (Е =1).
В тригонометрической форме ряд Фурье:
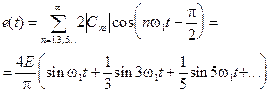 (3.37)
(3.37)
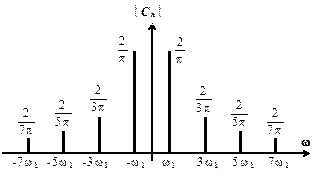
Рис. 3.3. Комплексный ряд Фурье, E =1
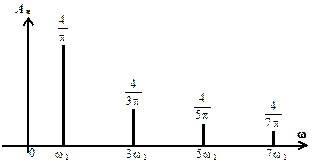
Рис. 3.4. Тригонометрический ряд Фурье, E =1
При отсчете времени от середины импульса, функция является четной относительно t и ряд для нее содержит только косинусные члены:
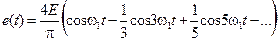 (3.38)
(3.38)
Для конечной суммы ряда, с увеличением числа суммируемых гармоник, сумма ряда приближается к функции e (t) всюду, кроме точек разрыва функции, где образуются выбросы. При n ®¥ величина этого выброса равна 1.18 Е, то есть сумма ряда отличается от заданной функции на 18%.
Этот дефект сходимости в математике получил название явления Гиббса в честь Дж. Уилларда Гиббса. Открытие этого эффекта не принадлежит Гиббсу, однако он первый «разрекламировал» этот эффект. Несмотря на то, что в рассматриваемом случае ряд Фурье не сходится к разлагаемой функции e (t) в точках ее разрыва, ряд сходится в среднем, поскольку при n ®¥ выбросы являются бесконечно узкими и не вносят никакого вклада в интеграл (3.13).
На Рис. 3.5представлено формирование меандра суммой 1-ой и 3-ей гармоник, а на
Рис. 3.6 - сумма 1-ой, 3-ей и 5-ой гармоник.
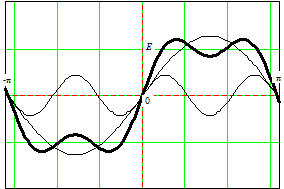
Рис. 3.5. Сумма 1 ой и 3 ей гармоник
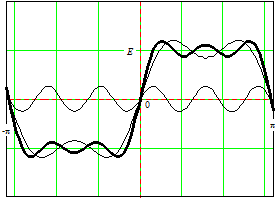
Рис. 3.6. Сумма 1,3 и 5 ой гармоник
Вычисление интеграла:
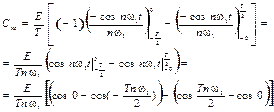
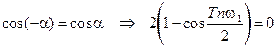
 2015-02-04
2015-02-04 3956
3956








