Приведем формулы расчета некоторых наиболее употребительных агрегатных индексов.
1) В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями 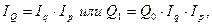 (8.9)
(8.9)
где 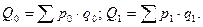
Если принимается предположение об очередности влияния факторов – сначала q, а затем р, то общий прирост товарооборота будет распределяться по факторам следующим образом:
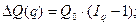
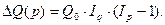
Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, то меняются и формулы разложения прироста и формулы расчета индексов Iq и Ip. Тогда
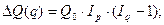
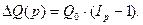
где 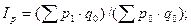
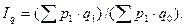
2) Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства (q) и затрат на единицу (z):
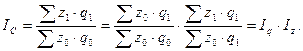 (8.10)
(8.10)
3) Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих (Т) и заработной платы (f):
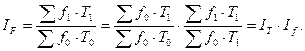 (8.11)
(8.11)
4) Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w):
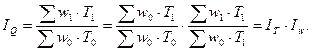 (8.12)
(8.12)
5) Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования – фондоотдачи (Н):
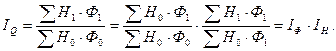 (8.13)
(8.13)
Аналогичным образом находят общие агрегатные индексы и по многим другим экономическим показателям. Нетрудно заметить, что используемые в приведенных формулах индексы Iq, IТ, Iф получаются по методу индекса физического объема, а индексы Iz, If, IW, IH – по методу индекса цен. Таким образом, рассмотренная выше методика распределения общего прироста товарооборота полностью приложима к анализу прироста продукции, изменения общих затрат на производство, изменения общего фонда оплаты труда и т.д.
Одним из важнейших показателей статистики цен, широко используемым в экономической и социальной политике, является индекс потребительских цен (ИПЦ). Он находит широкое использование при пересмотре социальных программ, служит основой для повышения минимального размера заработной платы, отражает реальную покупательную способность денег.
Методика расчета этого показателя включает отбор товаров (услуг) - представителей и торговых предприятий, по которым производится регистрация цен.
Индекс - дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного года, но определенного в ценах базисного года.
8.4 Средневзвешенные индексы
Агрегатный способ представления общих индексов в статистике является наиболее распространенным. Вместе с тем используется и другой подход расчета общих индексов как средних из соответствующих индивидуальных индексов, или средневзвешенных индексов.
К расчету средневзвешенных индексов обращаются в тех случаях, когда первичная (исходная) информация не позволяет рассчитать общий агрегатный индекс. Существует две формы средневзвешенных индексов: среднеарифметическая и среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический – при индексации качественных показателей (например, цен).
При расчете среднего арифметического индекса индексируемая величина числителя выражается через индивидуальный индекс.
Например, необходимо вычислить общий индекс физического объема продукции Iq, когда по исходным данным известны индивидуальные индексы физического объема (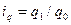 ) и стоимость продукции каждого вида за базисный период (
) и стоимость продукции каждого вида за базисный период (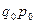 ). Тогда общий индекс физического объема продукции можно определить как среднюю арифметическую взвешенную из индивидуальных индексов. Для этого заменяем неизвестное количество продукции отчетного периода (
). Тогда общий индекс физического объема продукции можно определить как среднюю арифметическую взвешенную из индивидуальных индексов. Для этого заменяем неизвестное количество продукции отчетного периода (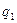 ) произведением
) произведением 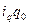 . Тогда общий индекс физического объема продукции приобретет вид:
. Тогда общий индекс физического объема продукции приобретет вид: 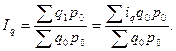 (8.14)
(8.14)
Эта формула представляет собой среднюю арифметическую из индивидуальных индексов физического объема продукции, взвешенную по стоимости продукции базисного периода.
Если индексируемая величина выражается через индивидуальный индекс в знаменателе, то индекс имеет название среднего гармонического индекса.
Например, известны индивидуальные индексы цен (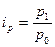 ) и стоимость каждого вида продукции за текущий (отчетный) период (
) и стоимость каждого вида продукции за текущий (отчетный) период (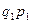 ), но неизвестны данные о цене единицы продукции за базисный период (
), но неизвестны данные о цене единицы продукции за базисный период (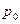 ). Чтобы найти средний гармонический индекс цен, цену базисного периода (
). Чтобы найти средний гармонический индекс цен, цену базисного периода (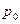 ) заменяем тождественным ей соотношением
) заменяем тождественным ей соотношением 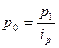 . Вследствие этого индекс цен будет иметь вид:
. Вследствие этого индекс цен будет иметь вид: 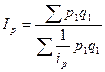 (8.15)
(8.15)
Эта формула представляет собой среднюю гармоническую из индивидуальных индексов цен, взвешенную по объему продукции текущего периода.
Пример. Имеются следующие данные:
| Вид изделия | Произведено в отчетном периоде, тыс. шт. q | Затраты на 1 изд, чел./час | |
| в отчетном периоде t1 | в базисном периоде t0 | ||
| А | 2,3 | ||
| Б | 1,5 | 1,8 | |
| В | 0,5 | 0,55 |
Индивидуальные индексы производительности труда (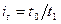 ) составят: по изд.А
) составят: по изд.А 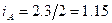 ; по изд.Б
; по изд.Б 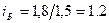 ; по изд.В
; по изд.В 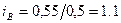 ;
;
Общий индекс производительности труда в агрегатной форме составит:
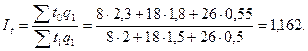
Общий индекс производительности труда как средний из индивидуальных индексов составит:
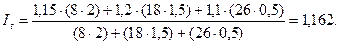
 2015-02-27
2015-02-27 873
873








