Формулы комбинаторики

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

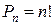, (2.3)

где ,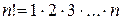

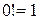
Пример 2

Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение: Искомое число трёхзначных чисел

.

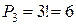Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

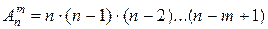(2.4)

Пример 3

Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

Решение. Искомое число сигналов

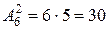. (2.5)

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые хотя бы одним элементом. Число сочетаний

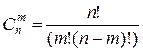(2.6)

Пример 4. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов

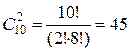(2.7)

Числа размещений, перестановок и сочетаний связаны равенством

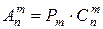(2.8)