Пусть производится n независимых испытаний в каждом из которых вероятность появления события А постоянна и равна p. Чему равно среднее число появлений события А в этих испытаниях?
Теорема
Математическое ожидание М(Х) числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
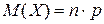 . (2.13)
. (2.13)
Пример 4
Вероятность попадания в цель при стрельбе из орудия 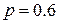 . Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.
. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.
Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание
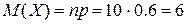 .
.
Если 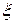 - случайная величина, то функция
- случайная величина, то функция
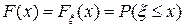 (2.14)
(2.14)
называется функцией распределения случайной величины 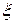 . Здесь -
. Здесь - 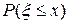 - вероятность того, что случайная величина
- вероятность того, что случайная величина 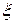 принимает значения, не превосходящие числа
принимает значения, не превосходящие числа 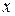 .
.
Функция распределения любой случайной величины обладает следующими свойствами:
· 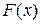 определена на всей числовой прямой R;
определена на всей числовой прямой R;
· 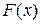 не убывает, т.е. если
не убывает, т.е. если 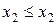 , то
, то 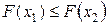 ;
;
· 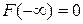 ,
, 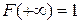 , т.е.
, т.е. 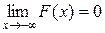 и
и 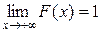
· 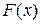 непрерывна справа, т.е.
непрерывна справа, т.е. 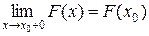
Функция распределения содержит всю информация об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения.
У дискретной случайной величины функция распределения ступенчатая.
Пример 5
Случайная величина принимает значение числа очков, выпавшее при однократном бросании кости. Определим ее функцию распределения:
Если 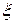 - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения 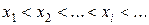 с вероятностями
с вероятностями 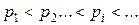 , то таблица вида
, то таблица вида
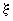
| 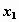
| 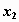
| ... | 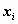
| ... |
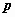
| 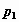
| 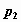
| ... | 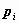
| ... |
называется распределением дискретной случайной величины.
Вероятность того, что значение случайной величины 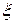 попадает в интервал
попадает в интервал 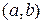 вычисляется для дискретной случайной величины по формуле:
вычисляется для дискретной случайной величины по формуле:
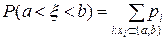 (2.15)
(2.15)
 2015-02-27
2015-02-27 439
439








