2015-02-27
540
Случайная величина х распределена по экспоненциальному закону, если плотность вероятности имеет вид
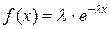, (2.20)
где х – случайная величина,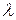 
- постоянная.
Если за случайную величину принять время работы до отказа изделия то выражение для плотности вероятности можно переписать в следующем виде:
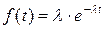, (2.21)
где t – время работы до отказа, 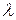- интенсивность отказов.
Для характеристик непрерывных распределений используется функция распределения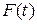 
:
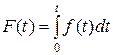. (2.22)
Подставив сюда выражение дл плотности вероятности, получим значение функции распределения для экспоненциального закона:
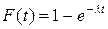. (2.23)
Физический смысл функции распределения 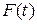- это вероятность того, что случайная величина попадает в интервал от 0 до t.
Экспоненциальный закон распределения характеризуется математическим ожиданием (среднее время наработки на отказ)
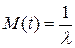. (2.24)
Экспоненциальный закон применяется только в тех случаях, когда наблюдается незначительный сбой в работе изделия, а отказы распределены равномерно в равных интервалах времени.
