В процессе приближенного отыскания корней уравнения обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня.
Локализация корня заключается в определении отрезка 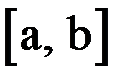 , содержащего один и только один корень. Не существует универсального алгоритма локализации корня. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции
, содержащего один и только один корень. Не существует универсального алгоритма локализации корня. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции 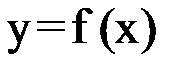 . На наличие корня на отрезке
. На наличие корня на отрезке 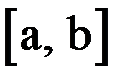 указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема.
указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема.
Теорема. Если функция 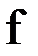 непрерывна на отрезке
непрерывна на отрезке 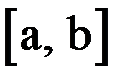 и принимает на его концах значения разных знаков так что
и принимает на его концах значения разных знаков так что 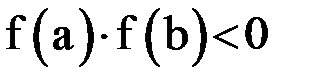 , то отрезок
, то отрезок 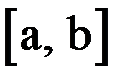 содержит по крайней мере один корень уравнения.
содержит по крайней мере один корень уравнения.
Однако корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция 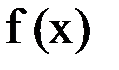 имеет постоянный знак. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью
имеет постоянный знак. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью 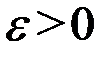 . Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений
. Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений 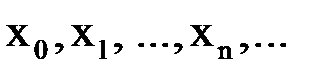 , которые являются приближениями к корню
, которые являются приближениями к корню 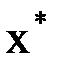 .
.
 2015-02-27
2015-02-27 308
308








